Вычислить площадь огорода имеющего форму прямоугольника

Калькулятор расчета площади земельного участка неправильной формы

Инструкция для калькулятора расчета площади неправильного земельного участка

Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме. Представленная программа способна правильно подсказать, как выполнить расчет площади земельных участков неправильной формы.

Важно! Важ участок должен приблизительно вписываться в окружность. Иначе расчеты будут не совсем точными.

Указываем все данные в метрах

A B, D A, C D, B C— Размер каждой стороны делянки.

Согласно введен данным, наша программа в онлайн режиме выполнить расчет и определить, площадь земельных угодий в квадратных метрах, сотках, акрах и гектарах.

Методика определения размеров участка ручным методом

Чтобы правильно выполнить расчет площади делянок, не нужно использовать сложные инструменты. Мы берем деревянные колышки или металлические прутья и устанавливаем их в углах нашего участка. Далее при помощи измерительной рулетки определяем ширину и длину делянки. Как правило, достаточно выполнить замер одной ширины и одной длины, для прямоугольных или равносторонних участков. Для примера, у нас получились следующие данные: ширина – 20 метров и длина – 40 метров.

Далее переходим к расчету площади делянки. При правильной форме участка, можно использовать геометрическую формулу определения площади (S) прямоугольника. Согласно этой формуле, нужно выполнить умножение ширины (20) на длину (40) , то есть произведение длин двух сторон. В нашем случае S=800 м².

После того, как мы определили нашу площадь, мы можем определить количество соток на земельном участке. Согласно общепринятым данным, в одной сотке – 100 м². Далее при помощи простой арифметики, мы разделим наш параметр S на 100. Готовый результат и станет равен размеру делянки в сотках. Для нашего примера, этот результат – 8. Таким образом, получаем, что площадь участка составляет восемь соток.

В том случае, когда территория угодий очень большая, то лучше всего выполнять все измерения в других единицах – в гектарах. Согласно общепринятым единицам измерения – 1 Га = 100 соток. К примеру, если наша земельная делянка согласно полученным измерениям составляем 10 000 м², то в этом случае его площадь равна 1 гектару или 100 соткам.

Если Ваш участок неправильной формы, то в этом случае количество соток напрямую зависит от площади. Именно по этой причине при помощи онлайн калькулятора Вы сможете правильно рассчитать параметр S делянки, и после этого разделив полученный результат на 100. Таким образом, Вы получите расчеты в сотках. Такой метод предоставляет возможность измерять делянки сложных форм, что весьма удобно.

Общие данные

Расчет площади земельных участков базируется на классических расчетах, которые выполняются согласно общепринятым геодезическим формулам.

Всего доступно несколько методов для расчета площади земельных угодий – механический (рассчитывается по плану при помощи мерных палеток), графический (определяется по проекту) и аналитический (при помощи формулы площади по измеренным линиям границ).

На сегодняшний день самым точным способом заслуженно считается – аналитический. Используя данный метод, ошибки при расчетах, как правило, появляются из-за погрешностей на местности измеренных линий. Данный способ является также и достаточно сложным, если границы криволинейные или количество углом на делянке больше десяти.

Немного проще по расчетам является графическим способ. Его лучше всего использовать в том случае, когда границы участка представлены в виде ломанной линии, с небольшим количеством поворотов.

И самый доступный и простой способ, и наиболее популярный, но и в тоже время самой большой погрешностью – механический способ. Используя данный метод, Вы сможете легко и быстро выполнить расчет площади земельных угодий простой или сложной формы.

Среди серьезных недостатков механического или графического способа, выделяют следующее, кроме погрешностей при измерении участка, при расчетах добавляется погрешность из-за деформации бумаги или погрешность при составлении планов.

Источник статьи: http://o-builder.ru/kalkulyator-ploshhadi-zemelnogo-uchastka/

§21. Площадь. Площадь прямоугольника — Ответы (ГДЗ) рабочая тетрадь (Мерзляк Полонский Якир) 5 класс часть 1

ПОВТОРЯЕМ ТЕОРИЮ

243. Заполните пропуски.

1) Равные фигуры имеют равные площади.
2) Площадь фигуры равна сумме площадей фигур , из которых она состоит.
3) За единицу измерения площади выбирают квадрат , сторона которого равна единичному отрезку .
4) Измерить площадь фигуры — значит подсчитать, сколько единичных квадратов в ней помещается.
5) 1 см 2 — это площадь квадрата со стороной 1 см .
6) 1 дм 2 — это площадь квадрата со стороной 1 дм .
7) Площадь прямоугольника вычисляют по формуле S= a*b , где S — его площадь , a и b — длины соседних сторон, выраженные в одних и тех же единицах .
8) Площадь квадрата вычисляют по формуле S= a 2 , где S — его площадь , a — его сторона .
9) 1 м 2 = 10000 см 2
10) 1 км 2 = 1000000 м 2
11) 1 а = 100 м 2
12) 1 га = 10000 м 2 = 100 а

РЕШАЕМ ЗАДАЧИ

244. Если стороны прмоугольника равны 12 см и 8 см, то его площадь

S = 12*8 = 96 см 2

245. Если сторона квадрата равна 9 дм, то его площадь

S = 9 2 = 81 дм 2

246. Заполните пропуски.

1) 6 а = 600 м 2
12 га = 120000 м 2
3 га 42 а = 34200 м 2

2) 7 га = 700 а
6 га 5 а = 605 а
72 000 м 2 = 720 а

3) 4 дм 2 = 400 см 2
4 м 2 = 40000 см 2
2 м 2 35 дм 2 = 23500 см 2

4) 270000 м 2 = 27 га
8000 а = 80 га
2 км 2 = 200 га

247. Сравните величины.

248. Заполните таблицу, где S — площадь прямоугольника, a и b — длины его соседних сторон.

а	3 дм	8 дм	40 см	5 км	36 см	30 м
b	6 см	5 дм	9 дм	4 м	6 дм	4 км
S	180 см 2	40 дм 2	36 дм 2	20 га	2160 см 2	12 а

1) 30 см*6 см = 180 см 2
2) 8 дм*5 дм = 40 дм 2
3) 40 см (4 дм)*9 дм = 36 дм 2
4) 5 км (5000 м)*4 м = 20000 км = 20 га
5) 36 см*6 дм (60 см) = 2160 см 2
6) 30 м*4 км(4000 м) = 120000 м = 12 а

249. Найдите площадь квадрата, периметр которого равен 64 см.

Решение:
1) 64:4 = 16 (см) длина сторон квадрата
2) 16*16 = 256 (см 2 ) площадь квадрата

Ответ: Площадь квадрата 256 см 2 .

250. Поле прмоугольной формы имеет площадь 42 а, его длина равна 70 м. Вычислите периметр поля.

Решение:
42 а = 42000 м 2
1) 42000:70 = 600 (м) ширина поля
2) 2*(70*600) = 2600 (м) периметр поля

Ответ: периметр поля равен 2600 м.

251. На рисунке изображен прямоугольник ABCD, у которого АD=8 см, АВ=4 см. Точка К — середина отрезка АD, точка М — середина отрезка АК, точка F — середина отрезка АВ, точка Е — середина отрезка АF. Чему равна площадь закрашенного прямоугольника?

Ответ: Площадь закрашенного прямоугольника равна 2 см 2 .

252. На рисунке изображены три квадрата. Середины сторон большого квадрата являются вершинами среднего квадрата, а середины сторон среднего квадрата — вершинами маленького квадрата. Площадь маленького квадрата равна 25 см 2 . Чему равна площадь квадрата?

Ответ: площадь квадрата равна 100 см 2

253. Вычислите площадь фигуры, изображенной на рисунке (размеры даны в сантиметрах).

Решение:
(12+3)*6-(2*2*3+2*2) = 74 (см 2 ) или
12*6+2*3-2*2 = 74 (см 2 )

Ответ: площадь фигуры равна 74 см 2 .

254. Заполните цепочку вычислений.

1) 600 а : 300 = 2 а
2) 2 а + 4 а = 6 а
3) 600 м 2 — 120 м 2 = 480 м 2
4) 48000 дм 2 : 800 = 60 дм 2
5) 60 дм 2 — 28 дм 2 = 32 дм 2

255. Сколько надо рулонов обоев, чтобы оклеить ими стену длиной 7 м и высотой 4 м, если длина рулона равна 10 м, а ширина — 50 см?

Решение:
1) 7*4 = 28 (м 2 ) площадь стены
2) 50*1000 = 50000 (см 2 ) = 5 (м 2 ) содержит улон обоев
3) 28:5 = 5 ост.3 (рулоны)

Ответ: 6 рулонов

256. С огорода, который имеет форму приямоугольника со сторонами 50 м и 30 м, собрали 180 ведер картофеля. В одно ведро помещается 8 кг картофеля. Сколько килограммов картофеля собрали с 1 а?

Решение:
1) 50*30 = 1500 (м 2 ) = 15 а — площадь огорода.
2) 180:15 = 12 (ведер) с одного а
3) 12*8 = 96 (кг) с одного а

Ответ: 96 кг с одного а.

257. Длина прямоугольника равна 28 см. На сколько квадратных сантиметров увеличится его площадь, если ширину этого прямоугольника увеличить на 3 см?

Решение:
28*(х+3)-28*х = 28х+28*3-28х = 28*3 = 84 (см 2 )

Ответ: площадь увеличится на 84 см 2 .

258. Во сколько раз увеличится периметр и во сколько раз увеличится площадь прямоугольника, если каждую его сторону увеличить в 3 раза?

Решение:
1) 2*(3а+3b):2(а+b) = 6а+6b:2а+2b = 6(а+b):2(а+b) = 6:2 = 3
2) (3а*3b):(а*b) = 9аb аb = 9

Ответ: в 3 раза; в 9 раз.

259. На рисунке изображен квадрат, разбитый на шесть прямоугольников, сумма периметров которых равна 80 см. Чему равна площадь квадрата?

S = а 2 = 10 2 = 100 (см 2 )

Ответ: площадь квадрата равна 100 см 2 .

Источник статьи: http://matem-gdz.ru/5-klass/otvety-gdz-rabochaya-tetrad-merzlyak-polonskij-yakir-5-klass-chast-1/21.-ploshhad.-ploshhad-pryamougolnika.html

Мерзляк 5 класс — § 21. Площадь. Площадь прямоугольника

Вопросы к параграфу

1. Какие свойства площади фигуры вы знаете?

1. Равные фигуры имеют равные площади.
2. Площадь фигуры равна сумме площадей фигур, из которых она состоит.

2. Какой квадрат называют единичным?

Единичный квадрат — это квадрат, стороны которого равны единичному отрезку.

3. Какие единицы измерения площади вы знаете?

• мм² — квадратный миллиметр
• см² — квадратный сантиметр
• м² — квадратный метр
• км² — квадратный километр

4. Что означает измерить площадь фигуры?

Измерить площадь фигуры — это значит подсчитать, сколько единичных квадратов в ней помещается.

5. Чему равна площадь прямоугольника?

Площадь прямоугольника равна произведению длин его соседних сторон:

S = ab

6. По какой формуле вычисляют площадь квадрата?

S = a²

7. Сколько квадратных метров содержит 1 ар? 1 гектар?

Решаем устно

1. Сколько сантиметров содержится в:

• 1 дм = 10 см
• 1 м 3 дм = 130 см
• 5 м 2 дм = 520 см
• 12 дм 5 см = 125 см
• 40 мм = 4 см

2. Лодка за 5 ч прошла 40 км. За сколько часов она пройдёт с той же скоростью 24 км?

1) 40 : 5 = 8 (км/ч) — скорость лодки.

2) 24 : 8 = 3 (ч) — потребуется дл преодоления 24 км.

3. Сколько литров воды может перекачать насос за 8 мин, если пять таких насосов за 6 мин перекачивают 450 л воды?

1) 450 : 6 = 75 (л/мин) — скорость работы пяти насосов.

2) 75 : 5 = 15 (л/мин) — скорость работы одного насоса.

3) 15 • 8 = 120 (литров) — воды перекачает один насос за 8 минут.

Ответ: 120 литров воды.

4. Какую цифру надо поставить вместо звёздочек, чтобы запись 1* + 3* + 5* = 111 стала верным равенством?

Вспомним таблицу умножения на 3 и подберём число, которое при умножении на 3 дает число, оканчивающееся на 1. Это число 7 (7 • 3 = 21).

Подставим цифру 7 в равенство:

17 + 37 + 57 = 111 — равенство верно.

Упражнения

564. 1) Сколько квадратных сантиметров содержит 1 дм²? 1 м²?

1 дм² = 10 см • 10 см = 100 см²

1 м²= 100 см • 100 см = 10 000 см²

2) Сколько квадратных метров содержит 1 км²?

1 км²= 1 000 м • 1 000 м = 1 000 000 м²

565. Вычислите площадь прямоугольника, соседние стороны которого равны 14 см и 8 см.

S = ab
S = 14 • 8 = 112 (см²)

Ответ: S = 112 см²

566. Вычислите площадь квадрата со стороной 7 дм.

S = a²
S = 7 • 7 = 49 (дм²)

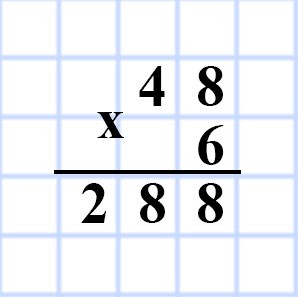
567. Одна сторона прямоугольника равна 16 см, а соседняя сторона — на 6 см длиннее. Вычислите площадь прямоугольника.

a = 16 см
b = (a + 6) см
S = ?

S = ab
S = 16 • (16 + 6) = 16 • 22 = 352 (см²)

Ответ: S = 352 см²

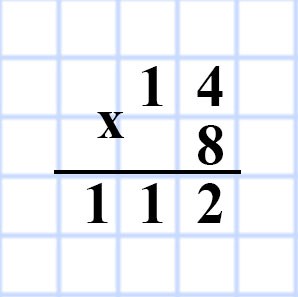
568. Одна сторона прямоугольника равна 48 см, а соседняя сторона — в 8 раз меньше. Вычислите площадь прямоугольника.

a = 48 см
b = (a : 8) см
S = ?

S = ab
S = 48 • (48 : 8) = 48 • 6 = 288 (см²)

Ответ: S = 288 см²

Внимание! Следующие 5 задач решены двумя способами!

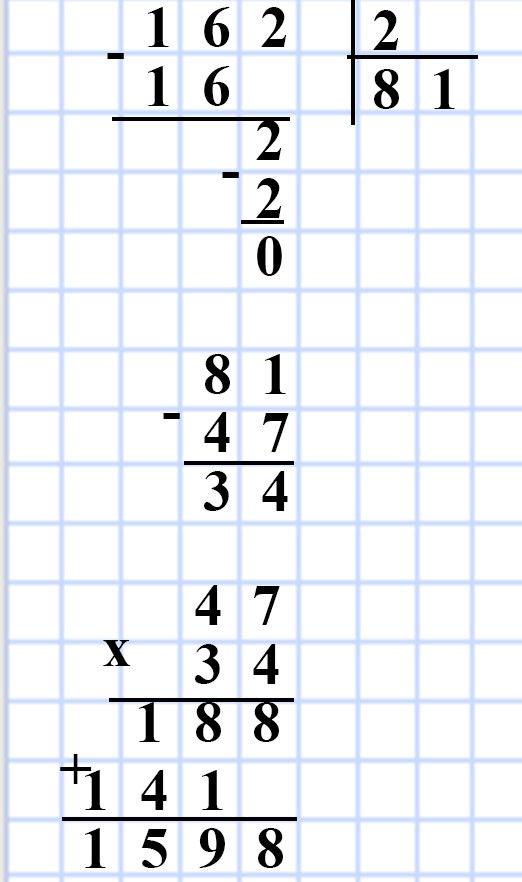
569. Периметр прямоугольника равен 162 дм, а одна из сторон — 47 дм. Найдите площадь прямоугольника.

Способ 1:

a = 47 дм
P = 162 дм
S = ?

P = (a + b) • 2
b = P : 2 — a
b = 162 : 2 — 47 = 81 — 47 = 34 (дм) — длина стороны b.

S = ab
S = 47 • 34 = 1 598 (дм²) — площадь прямоугольника.

Ответ: S = 1598 дм².

Способ 2:

1) 162 : 2 = 81 (дм) — сумма двух соседних сторон прямоугольника.

2) 81 — 47 = 34 (дм) — длина второй стороны прямоугольника.

3) 47 • 34 = 1 598 (дм²) — площадь прямоугольника.

Ответ: S = 1598 дм².

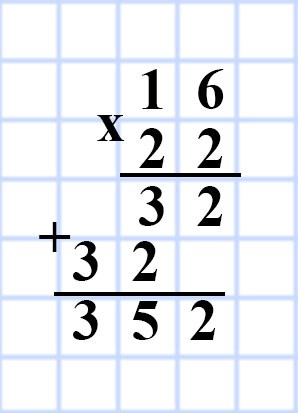
570. Периметр прямоугольника равен 96 м, и он в 8 раз больше одной из сторон прямоугольника. Найдите площадь прямоугольника.

Способ 1:

a = P : 8
a = 96 : 8 = 12 (м) — длина стороны a прямоугольника.

P = (a + b) • 2
b = P : 2 — a
b = 96 : 2 — 12 = 48 — 12 = 36 (м) — длина стороны b.

S = ab
S = 36 • 12 = 432 (м²) — площадь прямоугольника.

Способ 2:

1) 96 : 8 = 12 (м) — длина одной стороны прямоугольника.

2) 96 : 2 = 48 (м) — сумма длин соседних сторон прямоугольника.

3) 48 — 12 = 36 (м) — длина второй стороны прямоугольника.

4) 36 • 12 = 432 (м²) — площадь прямоугольника.

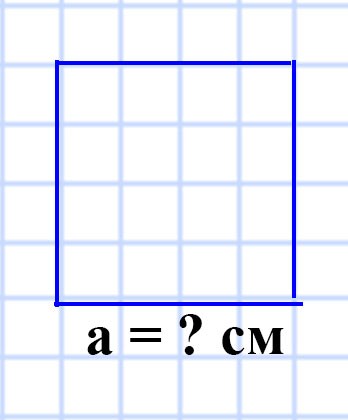
571. Найдите площадь квадрата, периметр которого равен 96 см.

Способ 1:

a = P : 4
a = 96 : 4 = 24 (см) — длина стороны квадрата.

S = a²
S = 24 • 24 = 576 (см²) — площадь прямоугольника.

Ответ: S = 576 см².

Способ 2:

1) 96 : 4 = 24 (см) — длина стороны квадрата.

2) 24² = 24 • 24 = 576 (см²) — площадь прямоугольника.

Ответ: S = 576 см².

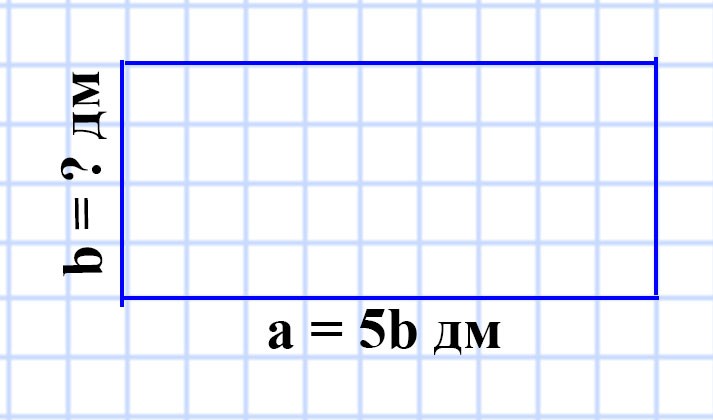
572. Периметр прямоугольника равен 4 м 8 дм, одна из его сторон в 5 раз больше соседней стороны. Найдите площадь прямоугольника.

Способ 1:

P = 4 м 8 дм
a = 5b
S = ?

4 м 8 дм = 48 дм

P = (a + b) • 2 и a = 5b. Составим уравнение:

48 = (5b + b) • 2
5b + b = 48 : 2
6b = 24
b = 24 : 6
b = 4 (дм) — длина стороны b прямоугольника

a = 5b = 5 • 4 = 20 (дм) — длина стороны a прямоугольника

S = ab
S = 20 • 4 = 80 (дм²) — площадь прямоугольника.

Способ 2:

4 м 8 дм = 48 дм

1) 48 : 2 = 24 (дм) — сумма длин соседних сторон прямоугольника.

2) 24 : 6 = 4 (дм) — длина одной стороны прямоугольника.

3) 4 • 5 = 20 (дм) — длина другой стороны прямоугольника.

4) 20 • 4 = 80 (дм²) — площадь прямоугольника.

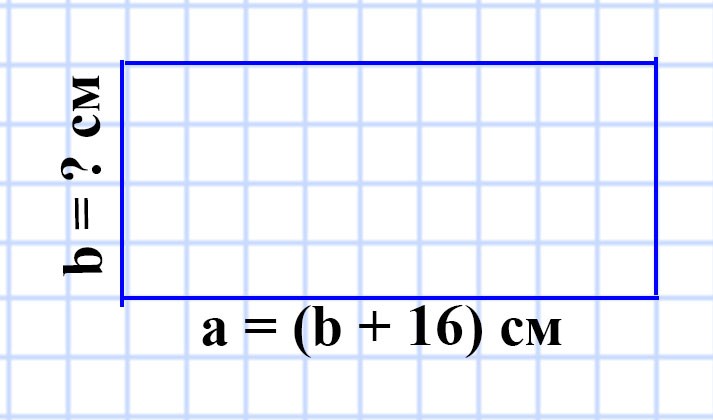
573. Периметр прямоугольника равен 6 дм 8 см, одна из его сторон на 1 дм 6 см меньше соседней стороны. Найдите площадь прямоугольника.

Способ 1

P = 6 дм 8 см
a = b + 1 дм 6 см
S = ?

6 дм 8 см = 68 см
1 дм 6 см = 16 см

P = (a + b) • 2 и a = b + 16 см. Составим уравнение:

68 = (b + 16 + b) • 2
b + 16 + b = 68 : 2
2b + 16 = 34
2b = 34 — 16
2b = 18
b = 18 : 2
b = 9 (см) — длина стороны b прямоугольника

a = b + 16 = 9 + 16 = 25 (см) — длина стороны a прямоугольника

S = ab
S = 25 • 9 = 225 (см²) — площадь прямоугольника.

Ответ: S = 225 см².

Способ 2:

6 дм 8 см = 68 см
1 дм 6 см = 16 см

1) 68 : 2 = 34 (см) — сумма длин двух соседних сторон прямоугольника.

2) 34 — 16 = 18 (см) — сумма длин двух коротких сторон прямоугольника.

3) 18 : 2 = 9 (см) — длина короткой стороны прямоугольника.

4) 34 — 9 = 25 (см) — длина длинной стороны прямоугольника.

5) 25 • 9 = 225 (см²) — площадь прямоугольника.

Ответ: S = 225 см².

574. Выразите:

1) в арах:

• 12 га = 1 200 а
• 45 га = 4 500 а
• 6 га 28 а = 600 а + 28 а = 628 а
• 14 га 68 а = 1 400 а + 68 а = 1468 а
• 32 400 м² = 324 а
• 123 800 м² = 1 238 а
• 2 км² 14 га 5 а = 20 000 а + 1 400 а + 5 а = 21 405 а
• 4 км² 72 га 16 а = 40 000 а + 7 200 а + 16 а = 47216 а

2) в квадратных метрах:

• 5 а = 500 м²
• 17 а = 1 700 м²
• 8 га = 80 000 м²
• 63 га = 630 000 м²
• 5 га 72 а = 50 000 м² + 7 200 м² = 57 200 м²
• 14 га 43 а = 140 000 м² + 4 300 м² = 144 300 м²

3) в гектарах и арах:

• 530 а = 5 га 30 а
• 1 204 а = 12 га 4 а
• 16 300 м² = 10 000 м² + 6 300 м² = 1 га 63 а
• 85 200 м² = 80 000 м² + 5 200 м² = 8 га 52 а

575. Выразите:

1) в квадратных сантиметрах:

• 8 дм² = 800 см²
• 16 дм² = 1 600 см²
• 4 м² = 40 000 см²
• 38 м² = 380 000 см²
• 16 м² 19 дм² = 160 000 см² + 1 900 см² = 161 900 см²
• 74 м² 3 дм² = 740 000 см² + 300 см² = 740 300 см²

2) в гектарах:

• 340 000 м² = 34 га
• 5 830 000 м² = 583 га
• 53 км² = 5 300 га
• 14 км² = 1 400 га
• 5 км² 18 га = 500 га + 18 га = 518 га
• 24 км² 6 га = 2 400 га + 6 га = 2 406 га

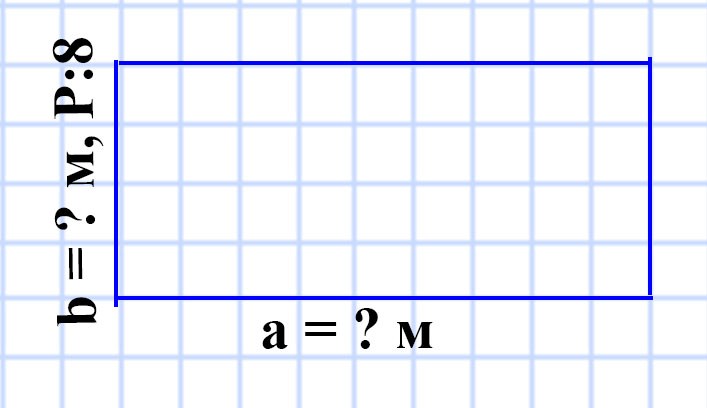
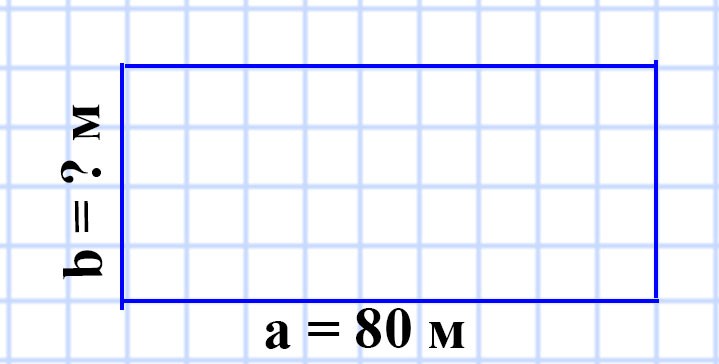
576. Поле прямоугольной формы имеет площадь 56 а, его длина — 80 м. Вычислите периметр поля.

a = 80 м
S = 56 а
P = ? м

S = ab
b = S : a = 5 600 : 80 = 70 (м) — ширина поля.

P = (a + b) • 2 = (70 + 80) • 2 = 150 • 2 = 300 (м) — периметр поля

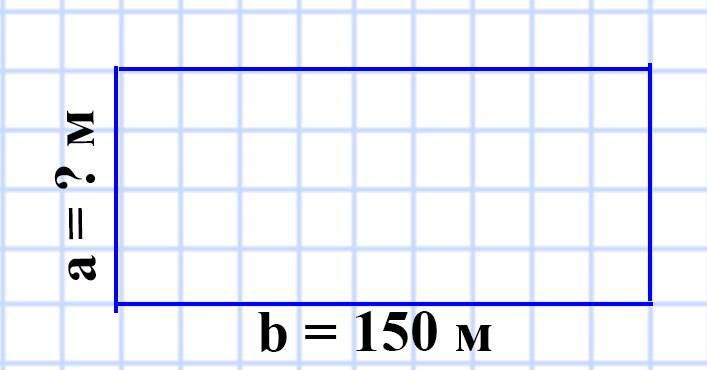
577. Поле прямоугольной формы имеет площадь 48 а, его ширина — 150 м. Вычислите периметр поля.

b = 150 м
S = 48 а
P = ? м

S = ab
a = S : b = 4 800 : 150 = 32 (м) — длина поля.

P = (a + b) • 2 = (32 + 150) • 2 = 182 • 2 = 364 (м) — периметр поля

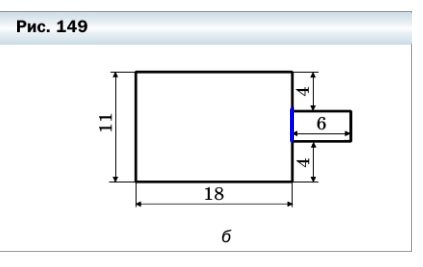
578. Вычислите периметр и площадь фигуры, изображённой на рисунке 149 (размеры даны в сантиметрах).

а)

1) Проведём вспомогательную линию и разделим фигуру на два прямоугольника.

2) Периметр фигуры равен сумме длин всех её сторон. Мы помним, что противоположные стороны прямоугольника равны. Значит:

• 15 — 5 = 10 (см) — длина части большого прямоугольника, не обозначенная на схеме и не равная стороне этого прямоугольника.

P = 15 + 18 + 10 + 8 + 5 + 8 + 18 = 82 (см) — периметр всей фигуры.

3) Площадь фигуры равна сумме площадей фигур, из которых она состоит.

• Найдём площадь маленького прямоугольника: S = ab = 8 • 5 = 40 (см²).
• Найдём площадь большого прямоугольника: S = ab = 18 • 15 = 270 (см²).

Значит площадь всей фигуры: S = S (маленького прямоугольника) + S (большого прямоугольника) = 40 + 270 = 310 (см²).

Ответ: P = 82см, S = 310 см².

б)

1) Проведём вспомогательную линию и разделим фигуру на два прямоугольника.

2) Периметр фигуры равен сумме длин всех её сторон. Мы помним, что противоположные стороны прямоугольника равны. Значит:

• 11 — (4 + 4) = 3 (см) — ширина маленького прямоугольника.

P = 18 + 4 + 6 + 3 + 6 + 4 + 18 + 11 = 70 (см) — периметр всей фигуры.

3) Площадь фигуры равна сумме площадей фигур, из которых она состоит.

• Найдём площадь маленького прямоугольника: S = ab = 6 • 3 = 18 (см²).
• Найдём площадь большого прямоугольника: S = ab = 18 • 11 = 198 (см²).

Значит площадь всей фигуры: S = S (маленького прямоугольника) + S (большого прямоугольника) = 18 + 198 = 216 (см²).

Ответ: P = 70 см, S = 216 см².

579. Вычислите периметр и площадь фигуры, изображённой на рисунке 150 (размеры даны в сантиметрах).

1) Проведём вспомогательную линию(синюю) и разделим фигуру на три прямоугольника.

2) Периметр фигуры равен сумме длин всех её сторон. Мы помним, что противоположные стороны прямоугольника равны. Значит:

• 12 + 6 + 12 = 30 (см) — длина большого прямоугольника.
• 18 — 4 = 14 (см) — ширина большого прямоугольника.

P = 12 + 4 + 6 + 4 + 12 + 18 + 30 + 18 = 104 (см) — периметр всей фигуры.

3) Площадь фигуры равна сумме площадей фигур, из которых она состоит.

• Найдём площадь первого маленького прямоугольника: S = ab = 12 • 4 = 48 (см²).
• Найдём площадь второго маленького прямоугольника: S = ab = 12 • 4 = 48 (см²).
• Найдём площадь большого прямоугольника: S = ab = 30 • 12 = 420 (см²).

Значит площадь всей фигуры: S = S (маленького первого прямоугольника) + S (маленького второго прямоугольника) + S (большого прямоугольника) = 48 + 48 + 420 = 516 (см²).

Ответ: P = 104 см, S = 516 см².

Комментарий: Площадь данной фигуры удобнее находить другим способом. Для этого надо провести вторую вспомогательную линию (красную) и из площади получившегося в результате построения большого прямоугольника вычесть площадь маленького прямоугольника:

• Найдём площадь большого прямоугольника: S = ab = 30 • 18 = 540 (см²).
• Найдём площадь маленького прямоугольника: S = ab = 6 • 4 = 24 (см²).

Значит площадь всей фигуры: S = S (большого прямоугольника) — S (маленького прямоугольника) = 540 — 24 = 516 (см²).

580. Хватит ли 5 т гороха, чтобы засеять им поле, имеющее форму прямоугольника со сторонами 500 м и 400 м, если на 1 га земли надо высеять 260 кг гороха?

1) 500 • 400 = 200 000 м² = 20 га — площадь поля.

2) 260 • 20 = 5 200 (кг) — гороха потребуется для засеивания поля.

3) 5 200 кг >5 000 кг — значит 5т гороха не хватит для засеивания поля.

Ответ: Нет, не хватит.

581. Отец решил облицевать кафелем стену кухни, длина которой равна 4 м 50 см, а высота — 3 м. Хватит ли ему 20 ящиков кафеля, если одна плитка имеет форму квадрата со стороной 15 см, а в одном ящике находится 30 плиток?

• 4м 50 см = 450 см — длина стены
• 3 м = 300 см — высота стены

1) 15 • 15 = 225 (см²) — площадь 1 плитки.

2) 450 • 300 = 135 000 (см²) — площадь стены.

3) 135 000 : 225 = 600 (шт) — плиток потребуется на облицовку стены.

4) 30 • 20 = 600 (шт) — плиток находится в 20 ящиках.

5) 600 шт = 600 шт — значит 20 ящиков плитки хватит для облицовки стены.

Ответ: Да, хватит.

582. Фермер Пётр Трудолюб посадил в теплице огурцы. Длина теплицы равна 16 м 50 см, а ширина — 12 м. Сколько килограммов огурцов соберёт фермер в своей теплице, если с 1 м² собирают 30 кг огурцов?

• 16 м 50 см = 1 650 см
• 12 м = 1 200 см

1) 1 650 • 1 200 = 1 980 000 см² = 198 м² — площадь теплицы.

2) 198 • 30 = 5 940 (кг) — огурцов соберёт фермер.

Ответ: 5 940 кг огурцов.

583. Расход эмалевой краски на однослойное покрытие составляет 180 г на 1 м². Хватит ли 3 кг эмали, чтобы покрасить стену длиной 6 м и высотой 3 м?

1) 6 • 3 = 18 (м²) — площадь стены.

2) 18 • 180 = 3 240 (г) — краски потребуется на однослойное покрытие стены.

3) 3 240 г > 3 000 г — значит 3 кг краски не хватит на окраску данной стены.

Ответ: Нет, не хватит.

584. Квадрат со стороной 12 см и прямоугольник, длина которого равна 18 см, являются равновеликими. Найдите периметр прямоугольника.

1) 12 • 12 = 144 (см²) — площадь квадрата = площадь прямоугольника.

2) 144 : 18 = 8 (см) — длина стороны b прямоугольника.

3) (18 + 8) • 2 = 26 • 2 = 52 (см) — периметр прямоугольника.

585. Квадрат и прямоугольник являются равновеликими, соседние стороны прямоугольника равны 3 см и 12 см. Найдите периметр квадрата.

1) 12 • 2 = 36 (см²) — площадь прямоугольника = площадь квадрата.

2) Подберём число, квадрат которого равен 36. Это число 6 (6 • 6 = 36). Значит сторона квадрата равна 6 см.

3) 6 • 4 = 24 (см) — периметр квадрата.

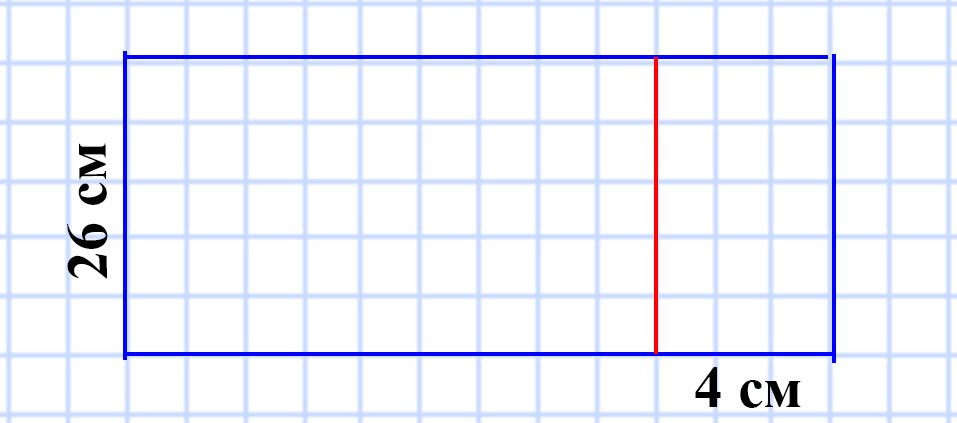
586. Ширина прямоугольника равна 26 см. На сколько квадратных сантиметров увеличится площадь этого прямоугольника, если его длину увеличить на 4 см?

Для того, чтобы узнать на сколько квадратных сантиметров увеличится площадь этого прямоугольника, надо найти площадь маленького прямоугольника, полученного в результате увеличения длины на 4 см.

Мы знаем, что противоположные стороны прямоугольника равны.

26 • 4 = 104 (см²) — площадь, на которую увеличиться площадь исходного прямоугольника.

Ответ: на 104 см².

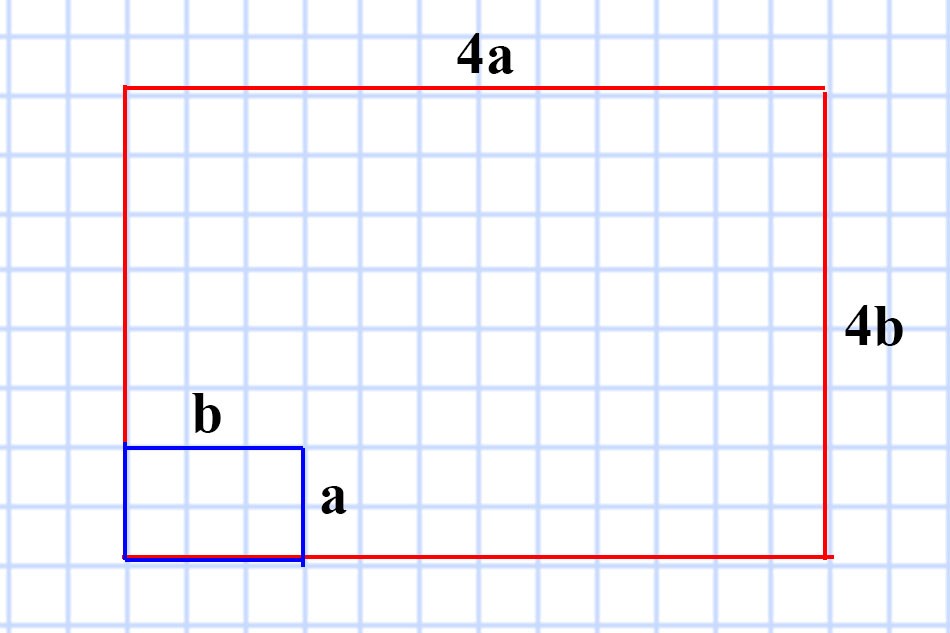
587. Во сколько раз увеличатся периметр и площадь прямоугольника, если каждую его сторону увеличить в 4 раза?

Посчитаем, во сколько раз увеличится периметр прямоугольника, если каждую его сторону увеличить в 4 раза.

• P (исходного прямоугольника) = (a + b) • 2 = 2(a + b)
• P (увеличенного прямоугольника) = (4a + 4b) • 2 = 8(a + b)

8(a + b) : 2(a + b) = 4 (раза) — увеличился периметр прямоугольника.

Посчитаем, во сколько раз увеличится площадь прямоугольника, если каждую его сторону увеличить в 4 раза.

• S (исходного прямоугольника) = ab
• S (увеличенного прямоугольника) = 4a • 4b = 16ab

16ab : ab = 16 (раз) — увеличится площадь прямоугольника.

Ответ: Периметр увеличится в 4 раза, а площадь увеличится в 16 раз.

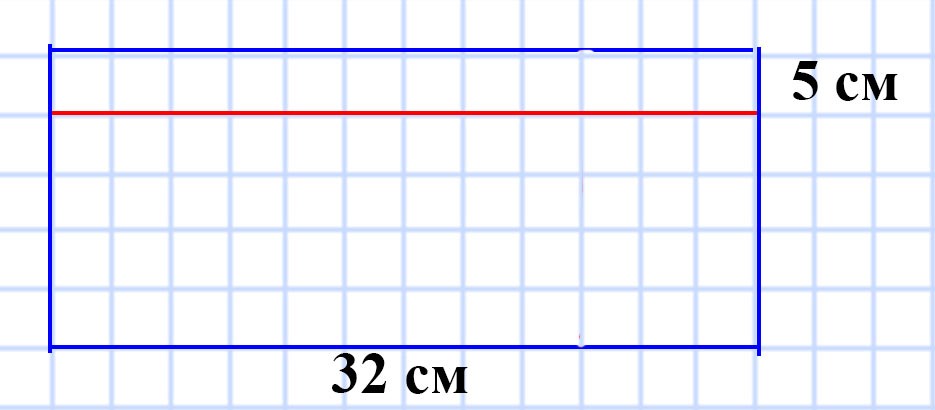
588. Длина прямоугольника равна 32 см. На сколько квадратных сантиметров уменьшится площадь этого прямоугольника, если его ширину уменьшить на 5 см?

Для того, чтобы узнать на сколько квадратных сантиметров увеличится площадь этого прямоугольника, надо найти площадь маленького прямоугольника, полученного в результате увеличения ширины на 5 см.

Мы знаем, что противоположные стороны прямоугольника равны.

32 • 5 = 160 (см²) — площадь, на которую увеличиться площадь исходного прямоугольника.

Ответ: на 160 см².

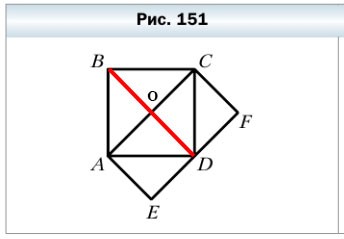
589. Площадь квадрата ABCD равна 16 см² (рис. 151). Чему равна площадь прямоугольника ACFE?

1) Проведём в квадрате ABCD ещё одну диагональ BD. Каждая из диагоналей делит квадрат ABCD на 2 равные части, а две диагонали AC и BD делят квадрат ABCD на 4 равных треугольника. Значит:

2) AODE — квадрат, так как две его соседние стороны AO и OD равны. Диагональ AD делит квадрат AODE на 2 равных треугольника. Значит:

2) OCFD — квадрат, так как две его соседние стороны OD и OC равны. Диагональ CD делит квадрат OCFD на 2 равных треугольника. Значит:

Ответ: площадь прямоугольника ACFE равна 16 см².

590. Стороны прямоугольного листа бумаги имеют целочисленную длину (в сантиметрах), а площадь листа равна 12 см². Сколько квадратов площадью 4 см² можно вырезать из этого прямоугольника?

1) Если площадь листа равна 12 см², то лист может быть следующих форматов:

• 1 см х 12 см
• 2 см х 6 см
• 3 см х 4 см

2) Если площадь квадрата равна 4 см², то его сторона может быть равна только 2 см, так как 2 • 2 = 4 см².

3) Из листа со сторонами 1 см х 12 см невозможно вырезать ни одного квадрата со стороной 2 см.

4) Из листа со сторонами 2 см х 6 см можно вырезать 3 квадрата со стороной 2 см, так как:

• по длине 6 : 2 = 3
• по ширине 2 : 2 = 1
• 3 • 1 = 3

5) Из листа со сторонами 3 см х 4 см можно вырезать 2 квадрата со стороной 2 см, так как:

• по длине 4 : 2 = 2
• по ширине 3 : 2 = 1 (остаток 1).
• 2 • 1 = 2

Ответ: из листа площадью 12 см² можно вырезать 3 квадрата площадью 4 см², если стороны листа равны 2 и 6 см, либо 2 квадрата площадью 4 см², если стороны листа равны 3 и 4 см.

591. Стороны прямоугольного листа бумаги имеют целочисленную длину (в сантиметрах), а площадь листа равна 18 см². Сколько квадратов со стороной 3 см можно вырезать из этого листа?

1) Если площадь листа равна 18 см², то лист может быть следующих форматов:

• 1 см х 18 см
• 2 см х 9 см
• 3 см х 6 см

2) Из листа со сторонами 1 см х 18 см невозможно вырезать ни одного квадрата со стороной 3 см.

3) Из листа со сторонами 2 см х 9 см невозможно вырезать ни одного квадрата со стороной 3 см.

4) Из листа со сторонами 3 см х 6 см можно вырезать 2 квадрата со стороной 2 см, так как:

• по длине 6 : 3 = 2
• по ширине 3 : 3 = 1.
• 2 • 1 = 2

Ответ: из листа площадью 18 см² можно вырезать 2 квадрата со стороной 3 см, если стороны листа равны 3 и 6 см.

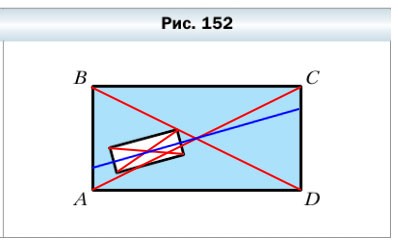
592. Внутри прямоугольника ABCD (рис. 152) вырезали отверстие прямоугольной формы. Как одним прямолинейным разрезом разделить полученную фигуру на две фигуры с равными площадями?

1. Проведём две вспомогательные линии (красные) и найдём точку пересечения диагоналей малого прямоугольника.
2. Проведём две вспомогательные линии (красные) и найдём точку пересечения диагоналей большого прямоугольника.
3. Проведём прямую (синяя) через две точки:
   • точку пересечения диагоналей малого прямоугольника
   • точку пересечения диагоналей большого прямоугольника.
4. Вдоль данной прямой выполним разрез и получим две фигуры с равными площадями.

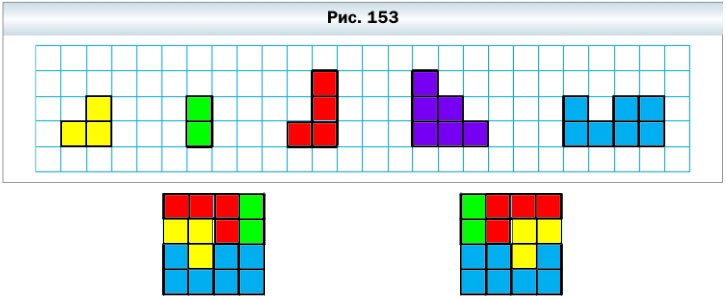
593. Используя четыре из пяти изображённых на рисунке 153 фигур, составьте квадрат.

594. Можно ли разрезать квадрат на несколько частей так, чтобы потом из них можно было составить два квадрата, длины сторон которых выражаются целым числом сантиметров, если сторона данного квадрата равна:

1) 5 см

Да, можно, так как площадь квадрата со стороной 5 см равна 5² = 25 см, а число 25 можно выразить суммой двух квадратов целых чисел: 25 = 4² + 3².

Например, можно разрезать квадрат со стороной 5 см на 4 квадрата со стороной по 2 см и 9 квадратов со стороной 1 см, а затем сложить из них одни квадрат со стороной 4 см и один квадрат со стороной 3 см.

2) 6 см

Нет, такие квадраты составить нельзя, так как число площадь квадрата со стороной 6 см равна 6² = 36 см, а число 36 нельзя выразить суммой двух квадратов целых чисел.

Упражнения для повторения

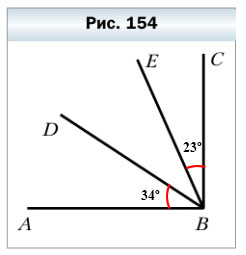
595. Из вершины прямого угла ABC (рис. 154) провели лучи BD и BE так, что угол АВЕ оказался больше угла DBE на 34º, а угол CBD больше угла DBE на 23º. Какова градусная мера угла DBE?

∠ABC= 90º — прямой

1) ∠ABD = ∠АВЕ — ∠DBE = 34º

2) ∠EBC ∠CBD — ∠DBE = 23º

3) ∠DBE = ∠ABC — ∠ABD — ∠EBC = 90º — 34º — 23º = 33º

596. Выполните действия:

Задача от мудрой совы

597. Расстояние между городами А и В равно 30 км. Из города А в город В выехал велосипедист и двигался со скоростью 15 км/ч. Одновременно из города В в направлении города А вылетела птица со скоростью 30 км/ч. Встретившись с велосипедистом, птица развернулась и полетела назад. Прилетев в город В, она снова развернулась и полетела навстречу велосипедисту. Встретившись с ним, птица развернулась и полетела назад в город В и т. д. Сколько километров пролетела птица за то время, пока велосипедист ехал из города А в город В?

1) 30 : 15 = 2 (часа) — потребуется велосипедисту, чтобы доехать из города А в город В.

Птица летала до места встречи с велосипедистом и обратно несколько раз все эти два часа, причём скорость полёта птицы была неизменна — 30 км/ч.

2) 30 • 2 = 60 (км) — пролетела птица в то время, пока велосипедист ехал из города А в город В.

Источник статьи: http://matem1234.ru/uc-merzlak-5-21/