Теория_графов_дерево_лес

Деревья и лес в теории графов

Дерево — это связный ациклический граф .Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути.

Лес — упорядоченное множество упорядоченных деревьев.

Ориентированное (направленное) дерево — ацикличный орграф ( ориентированный граф , не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.

Содержимое разработки

Определение. Н–граф называется неориентированным деревом (или просто деревом) если он связен и не содержит циклов, а значит петель и кратных ребер. Дерево – это минимальный связный граф в том смысле, что при удалении хотя бы одного ребра он теряет связность. Наличие этих двух свойств (связность и отсутствие циклов) позволяет жестко связать число вершин и число ребер: в дереве с вершинами всегда ребер. Пример графа–дерева приведен на рисунке 3.13. В этом графе 8 вершин и 7 ребер. Ни одно ребро нельзя удалить из графа без того, чтобы он не потерял связность.

Вершина графа называется концевой или висячей, если В графе на рис. 3.13 концевыми являются вершины .

Неориентированный граф–дерево может быть превращен в ориентированный. Ориентация неориентированного дерева проводится следующим образом. В дереве выбирается вершина – так называемый корень дерева , и все ребра такого дерева с корнем ориентируются от этой вершины – корня. Для каждой выбранной вершины ориентация дерева единственна, все ребра ориентированы от корня. Если изменить направления всех ребер ориентированного дерева (к корню) получим ориентированный граф, который иногда называют сетью сборки.

В каждую вершину ориентированного дерева (за исключением корня) входит только одно ребро. Любое дерево можно ориентировать, выбрав в качестве корня любую его вершину.

Пусть – вершина дерева с корнем , – множество всех вершин, связанных с корнем цепями, проходящими через вершину . Это множество порождает подграф , который называется ветвью вершины в дереве с корнем . Например, ветвью вершины на рис. 3.13 является подграф , содержащий вершины и ребра .

Определение. Лес – несвязный н–граф без циклов. Связные компоненты леса являются деревьями. Любая часть леса также является лесом или деревом. В неориентированном дереве между любыми двумя вершинами существует цепь и притом только одна.

Рассмотрим пример использование графа–дерева для решения задачи поиска гамильтоновых путей на взвешенном по ребрам графе, приведенном на рис. 3.14. Веса можно рассматривать как некоторый эквивалент затрат, связанных с переходом по ребру из одной вершины в другую. Будем считать, что коммивояжер отправляется из вершины , с тем, чтобы посетить вершины и вновь вернуться в .

Для решения задачи удобно воспользоваться вспомогательным графом–деревом, который позволяет не только получить все гамильтоновы пути, но и отслеживать вес каждого пути. Методика построения следующая: выделяется исходная вершина и ей присваивается нулевой вес. На вспомогательном графе такая вершина помечается как . Из исходной вершины проводятся ребра во все смежные вершины, по которым маршрут еще не проходил. Новым вершинам присваиваются веса, равный затратам, которые необходимо понести для их достижения из исходной вершины. Для рассматриваемого примера результатом первого шага станут вершины . Далее точно таким же образом производятся шаги из вновь полученных вершин, пока эти пути не приведут в исходную вершину. Часть путей могут быть тупиковыми, так как не позволяют завершить маршрут не заходя дважды в одну и ту же вершину. В данном примере, в частности, последовательность вершин является тупиковой.

Рис. 3.15. Граф–дерево, соответствующий полному перебору вариантов построения гамильтонового цикла в исходном графе рис. 3.14.

Приведенный на рис. 3.15 граф–дерево построен для решения задачи поиска кратчайшего гамильтонового пути с использованием метода полного перебора вариантов.

Проблема, однако, в том, что при большом числе вершин полный перебор вариантов, это работа, требующая огромных вычислений. В частности, для полного графа с вершинами число маршрутов равно . Если 5!=120, то 10!=3 628 800. И все-таки перебор маршрутов иногда бывает полезен. Известен метод решения задачи, в соответствии с которым шаг за шагом строится не полное, а «усеченное» дерево – часть ветвей в процессе его «выращивания» отсекаются, а оставшиеся ветви ведут к решению. Этот метод называется методом ветвей и границ.

Идея метода достаточно очевидна – каким-либо образом выбрать на графе некоторый путь, желательно покороче, а затем отбрасывать все варианты, которые явно длиннее. Простейшим алгоритмом может быть продолжение движения из вершины, имеющей минимальный вес. В рассмотренном примере, после первого шага, движение должно быть продолжено из вершины с наименьшим весом , что приводит в вершины и .

Выигрыш состоит в том, что неподходящие варианты просматриваются не до конца, а лишь до того момента, когда становится ясно, что рассматриваемый вариант хуже имеющегося. Общая полезность такого подхода зависит от степени дифференциации различных маршрутов, и от удачности построения первого маршрута. Ясно также, что в самом плохом случае мы получим полный перебор вариантов.

-82%

Источник

§ 3.8. Деревья, лес

Определение 3.8.1. Неориентированным деревом (или просто деревом) называется связный граф без циклов. Дерево есть связный граф, содержащий n вершин и n – 1 ребер, дерево есть граф, любые две вершины которого можно соединить простой цепью.

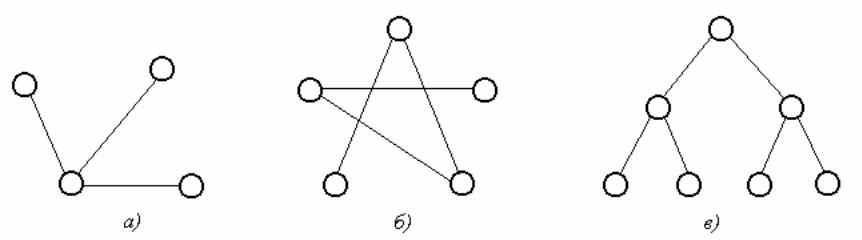
Пример. Графы, изображенные на рис 21, являются деревьями.

рис.21

Если граф несвязный и не имеет циклов, то каждая его связная компонента будет деревом. Такой граф называется лесом. Можно интерпретировать рис.21 как лес, состоящий из трех деревьев.

Определение 3.8.2. Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

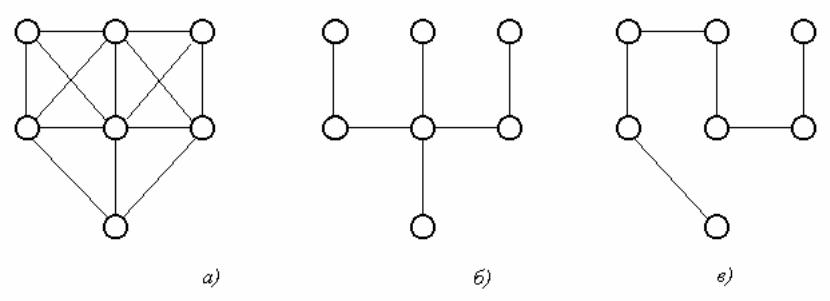
Пример. Для графа, изображенного на рис. 22 а), графы на рис. б и в являются остовными деревьями.

рис.22

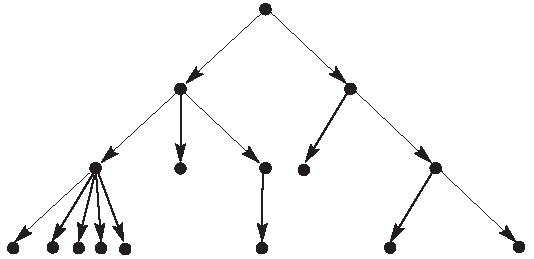
Определение 3.8.3. Ориентированным деревом называют граф, в котором в каждую вершину, кроме одной, называемой корнем дерева, заходит ровно одна дуга. В корень дерева ни одна дуга не заходит. Вершины, из которых не выходит ни одна дуга, называются листьями (рис.23).

рис.23

§ 3.9. Взвешенные графы

Определение 3.9.1. Взвешенный граф – это граф дугам, которого поставлены в соответствие веса, так что дуге (x_i, x_j) сопоставлено некоторое число c (x_i, x_j) = c_ij, называемое длиной (или весом, или стоимостью) дуги. Обычный (не взвешенный) граф можно интерпретировать как взвешенный, все ребра которого имеют одинаковый вес 1.

Определение 3.9.2. Длина пути во взвешенном графе — это сумма длин (весов) тех ребер, из которых состоит путь.

Определение 3.9.3. Расстояние между вершинами – это длина кратчайшего пути. Например, расстояние от вершины a до вершины d во взвешенном графе, изображенном на рис. 24, равно 6.

рис.24

Примеры взвешенных графов

§ 3.10. Эйлеровы и гамильтоновы графы

Определение 3.10.1. Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется эйлеровым циклом, а граф называется эйлеровым графом.

Определение 3.10.2. Если граф имеет цепь (не обязательно простую), содержащую все вершины по одному разу, то такая цепь называется эйлеровой цепью, а граф называется полуэйлеровым графом.

Эти понятия возникли в статье Эйлера в 1735 г., в которой он решал задачу о Кенигсбергских мостах и впервые ввел понятие графа. На рис.25, а приведен план расположения семи мостов в Кенигсберге (ныне Калининграде). Задача состоит в том, чтобы пройти каждый мост по одному разу и вернуться в исходную точку С. Поскольку в конце обхода нужно вернуться в исходную часть города, и на каждом мосту нужно побывать по одному разу, этот маршрут является простым циклом, содержащим все ребра графа. В дальнейшем такие циклы и стали называть эйлеровыми, а графы, имеющие эйлеров цикл – эйлеровыми графами.

Эйлеров цикл можно считать следом пера, вычерчивающего этот граф, не отрываясь от бумаги. Таким образом, эйлеровы графы – это графы, которые можно изобразить одним росчерком пера, причем процесс такого изображения начинается и заканчивается в одной и той же точке.

Обнаружив, что в данном графе не существует циклических обходов, проходящих по всем ребрам по одному разу, Эйлер обратился к общей задаче: при каких условиях в графе можно найти такой цикл? Ответ на этот вопрос дает следующая теорема.

Теорема Эйлера. Чтобы в связанном неориентированном графе G существовал эйлеров цикл, необходимо и достаточно, чтобы число вершин нечетной степени было четным.

Определение 3.10.3. Гамильтоновой цепью графа называется его простая цепь, которая проходит через каждую вершину графа точно один раз.

Определение 3.10.4. Цикл графа, проходящий через каждую его вершину, называется гамильтоновым циклом.

Определение 3.10.5. Граф называется гамильтоновым, если он обладает гамильтоновым циклом.

Гамильтоновы графы применяются для моделирования многих практических задач, например, служат моделью при составлении расписания движения поездов. Основой всех таких задач служит классическая задача коммивояжера: коммивояжер должен совершить поездку по городам и вернуться обратно, побывав в каждом городе ровно один раз, сведя при этом затраты на передвижения к минимуму.

Графическая модель задачи коммивояжера состоит из гамильтонова графа, вершины которого изображают города, а ребра — связывающие их дороги. Кроме того, каждое ребро оснащено весом, обозначающим транспортные затраты, необходимые для путешествия по соответствующей дороге, такие, как, например, расстояние между городами или время движения по дороге. Для решения задачи необходимо найти гамильтонов цикл минимального общего веса.

Теорема Кёнига. В полном конечном графе всегда существует гамильтонов путь.

Если в графе G(X) с n вершинами для любой пары вершин x_i и x_j справедливо неравенство

где m(х_i), m(x_j) – степени вершин х_i и x_j, то граф G(X) имеет гамильтонову цепь.

Несмотря на сходство в определении эйлерова и гамильтонового циклов, соответствующие теории для этих понятий имеют мало общего. Критерий существования для эйлеровых циклов был установлен просто, для гамильтоновых циклов никакого общего правила неизвестно. Более того, иногда даже для конкретных графов бывает трудно решить, можно ли найти такой цикл. В принципе, поскольку речь идет о конечном числе вершин, задачу можно решить перебором, однако эффективного алгоритма неизвестно.

Источник