Сколько процентов от площади всего огорода занимает теплица огэ математика

ОГЭ, Математика.
Геометрия: Задача №2C468F

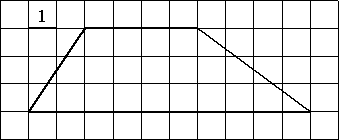
Найдите площадь трапеции, изображённой на рисунке.

Решение задачи:

Площадь трапеции равна произведению полусуммы оснований на высоту. Вычисляем:
S трапеции =3*(4+10)/2=21.
Ответ: S трапеции =21.

Вы можете поблагодарить автора, написать свои претензии или предложения на странице ‘Про нас’

Другие задачи из этого раздела

Задача №56CD5D

В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BMC.

Задача №649B05

В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.

Задача №0E3879

Площадь прямоугольного треугольника равна 512&#8730 3 . Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.

Задача №F7AB41

Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.

Задача №26768F

В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 67. Найдите площадь четырёхугольника ABMN.

Источник

ОГЭ, Математика.
Геометрия: Задача №0D90BE

Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 38°, 78° и 64°.

Решение задачи:

Пусть:
∠KMP=38°
∠MKP=78°
∠KPM=64°
Рассмотрим треугольник AMK.
AM=AK (по второму свойству касательной)
Следовательно треугольник AMK — равнобедренный, тогда, по свойству равнобедренного треугольника:
∠AMK=∠AKM
Заметим, что оба этих угла охватывают дугу MK, и следовательно равны половине ее градусной меры (по свойству углов на окружности).
∠MPK является вписанным в окружность углом и опирается на эту же дугу, следовательно и он равен половине градусной меры этой дуги.
Получается, что:
∠AMK=∠AKM=∠MPK=64°
Применив теорему о сумме углов треугольника:
180°=∠AMK+∠AKM+∠MAK
180°=64°+64°+∠MAK
∠MAK=52°
Аналогично, для двух других треугольников получим:
∠BKP=∠BPK=∠PMK=38°
∠KBP=180°-38°-38°=104°
И.
∠CPM=∠CMP=∠MKP=78°
∠PCM=180°-78°-78°=24°
Ответ: 52°, 104° и 24°

Вы можете поблагодарить автора, написать свои претензии или предложения на странице ‘Про нас’

Другие задачи из этого раздела

Задача №AE8E84

На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 2 м, высота фонаря 4 м?

Задача №EB43A2

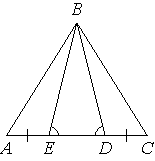
На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.

Задача №0A40BC

В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.

Задача №4081C6

Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 6 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.

Задача №E31D9C

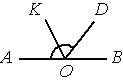
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.

Комментарии:

(2015-05-26 20:54:35) : Благодарю! (2015-05-20 08:06:59) Администратор: Киса, угол можно обозначать по разному, поэтому ∠PMK и ∠KMP — это одно и тоже. (2015-05-20 00:39:11) Киса: А почему у вас ∠BKP=∠BPK=∠PMK=38° вить вы писали, что ∠KMP=38°?

Найти задачу

Хочу получать новые решения

Источник

Сколько процентов от площади всего огорода занимает теплица огэ математика

Тип 4 № 408433

Сколько процентов от площади всего огорода занимает теплица?

На плане изображён дачный участок по адресу: п. Сосновка, ул. Зелёная, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв. м, а чуть подальше — жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведёт дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6).

Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером . Между гаражом и сараем находится площадка, вымощенная такой же плиткой.

К участку подведено электричество. Имеется магистральное газоснабжение.

Аналоги к заданию № 408432: 408433 408434 408786 Все

Тип 1 № 408405

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр без пробелов, запятых и других символов.

Объекты	жилой дом	баня	гараж	теплица
Цифры

Слева от ворот находится гараж, следовательно, он отмечен на плане цифрой 2. Справа от ворот находится сарай, значит, он отмечен на плане цифрой 1. Чуть дальше от сарая находится жилой дом, следовательно, он отмечен цифрой 7. Яблоневые посадки отмечены цифрой 3, баня — цифрой 4, теплица — цифрой 5, а огород цифрой — 6.

Тип 2 № 408413

Плитки для садовых дорожек продаются в упаковках по 10 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?

На дорожку приходится 25 плиток. Чтобы выложить площадку между сараем и гаражом необходимо: плиток. Следовательно, всего понадобится 65 плиток. Нужное количество плиток содержится в пачки. Округлив в большую сторону, получим ответ 7.

Тип 3 № 408424

Найдите периметр фундамента жилого дома. Ответ дайте в метрах.

Сторона одной клетки равна 2 м, значит, периметр фундамета жилого дома равен:

Тип 4 № 408432

Сколько процентов от площади всего участка занимают строения (жилой дом, гараж, сарай, баня)? Ответ округлите до целого.

Площадь всего участка является площадью прямоугольника со сторонами 20 м и 30 м. Следовательно, его площадь равна: Аналогично найдем площади строений. Гаража: сарая: бани: и жилого дома как сумму площадей двух прямоугольников: Всего постройки занимают От площади всего участка их общая площадь составляет

Тип 5 № 408438

Хозяин участка планирует установить в жилом доме систему отопления. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.

Нагреватель (котёл)	Прочее оборудование и монтаж	Средн. расход газа/ средн. потребл. мощность	Стоимость газа/ электроэнергии
Газовое отопление	20 000 руб.	15 370 руб.	1,6 куб. м/ч	4,9 руб./куб. м
Электр. отопление	15 000 руб.	14 000 руб.	4,9 кВт	4,2 руб./( кВтч )

Обдумав оба варианта, хозяин решил установить газовое отопление. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разницу в стоимости покупки и установки газового и электрического оборудования?

Чтобы установить газовое оборудование, понадобится Для установки электрического оборудования понадобится Разница в стоимости составляет

Час обогрева газом стоит Час обогрева электричеством стоит Разница в стоимости составляет

Значит, экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления через часов.

Источник

Сколько процентов от площади всего огорода занимает теплица огэ математика

Тип 4 № 408433

Сколько процентов от площади всего огорода занимает теплица?

На плане изображён дачный участок по адресу: п. Сосновка, ул. Зелёная, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв. м, а чуть подальше — жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведёт дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6).

Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером . Между гаражом и сараем находится площадка, вымощенная такой же плиткой.

К участку подведено электричество. Имеется магистральное газоснабжение.

Аналоги к заданию № 408432: 408433 408434 408786 Все

Тип 1 № 408405

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр без пробелов, запятых и других символов.

Объекты	жилой дом	баня	гараж	теплица
Цифры

Слева от ворот находится гараж, следовательно, он отмечен на плане цифрой 2. Справа от ворот находится сарай, значит, он отмечен на плане цифрой 1. Чуть дальше от сарая находится жилой дом, следовательно, он отмечен цифрой 7. Яблоневые посадки отмечены цифрой 3, баня — цифрой 4, теплица — цифрой 5, а огород цифрой — 6.

Тип 2 № 408413

Плитки для садовых дорожек продаются в упаковках по 10 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?

На дорожку приходится 25 плиток. Чтобы выложить площадку между сараем и гаражом необходимо: плиток. Следовательно, всего понадобится 65 плиток. Нужное количество плиток содержится в пачки. Округлив в большую сторону, получим ответ 7.

Тип 3 № 408424

Найдите периметр фундамента жилого дома. Ответ дайте в метрах.

Сторона одной клетки равна 2 м, значит, периметр фундамета жилого дома равен:

Тип 4 № 408432

Сколько процентов от площади всего участка занимают строения (жилой дом, гараж, сарай, баня)? Ответ округлите до целого.

Площадь всего участка является площадью прямоугольника со сторонами 20 м и 30 м. Следовательно, его площадь равна: Аналогично найдем площади строений. Гаража: сарая: бани: и жилого дома как сумму площадей двух прямоугольников: Всего постройки занимают От площади всего участка их общая площадь составляет

Тип 5 № 408438

Хозяин участка планирует установить в жилом доме систему отопления. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.

Нагреватель (котёл)	Прочее оборудование и монтаж	Средн. расход газа/ средн. потребл. мощность	Стоимость газа/ электроэнергии
Газовое отопление	20 000 руб.	15 370 руб.	1,6 куб. м/ч	4,9 руб./куб. м
Электр. отопление	15 000 руб.	14 000 руб.	4,9 кВт	4,2 руб./( кВтч )

Обдумав оба варианта, хозяин решил установить газовое отопление. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разницу в стоимости покупки и установки газового и электрического оборудования?

Чтобы установить газовое оборудование, понадобится Для установки электрического оборудования понадобится Разница в стоимости составляет

Час обогрева газом стоит Час обогрева электричеством стоит Разница в стоимости составляет

Значит, экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления через часов.

Источник