Шум перлина для генерации ландшафта

Шум Перлина: математика и генерация мира No Man’s Sky

Формулы, октавы и производные.

На конференции GDC 2017 выступил Шон Мюррей (Sean Murray), создатель No Man’s Sky — игры c процедурной генерацией контента. Он рассказал, как это работает на конкретных математических примерах.

​DTF публикует пересказ выступления.

Мюррей начинал в студии Criterion, сейчас принадлежащей EA. Тогда она славилась своими движками и технологиями. В основном Мюррей писал код. Потом он трудился над Burnout Paradise и Black, получившими (особенно за графику) хорошие отзывы.

Отдельно стоит упомянуть, что Мюррей участвовал в создании движка Renderware — он использовался в GTA, Call of Duty, Bully и других проектах. Разработчик даже оставил в них что-то вроде «авторской подписи»: баг, из-за которого у персонажей при определённых условиях отваливались руки.

По мнению Шона, движок игры определяет её дизайн. Сам выбор «мотора» — первый шаг в геймдизайне. К началу разработки No Man’s Sky Мюррей успел поучаствовать в создании семи игровых движков, так что и для неё решил сделать собственный.

Поначалу работа над No Man’s Sky была для него просто увлечением. Но существовавшие игровые движки казались слишком скучными, и он захотел сделать нечто принципиально новое.

No Man’s Sky перестала быть хобби после выхода первого трейлера. На момент выпуска видео игра настолько отличалась от всего, что было на рынке, что разработчикам было негде искать примеры решения проблем.

А их было немало: создание 3D-ландшафта с пещерами и нависающими частями, процедурное текстурирование, леса, строения и существа, горы высотой в несколько километров, планеты площадью в миллионы квадратных километров, разнообразные формы планет, NPC под управлением ИИ, способные путешествовать между небесными телами. К тому же, контент генерировался процедурно, так что его невозможно было протестировать.

В No Man’s Sky нельзя ничего «запечь» или рассчитать заранее. Простой пример: в любой другой игре, чтобы поставить маркер на крышу здания, достаточно расположить на карте строение, создать маркер и переместить его. А в No Man’s Sky движок должен учитывать изгиб планеты, иначе здание может оказаться под землёй или на другом её конце. Затем нужно разместить маркер на горизонте, потому что иначе его не будет видно. При этом ось Y не обозначает «высоту», поскольку планета — это реальный физический объект, так что нужно высчитывать тангенсы и касательные, а также расстояние до полюса планеты.

Итак, маркер на нужной высоте. Но что, если его нужно поставить на другую планету? Или, что ещё хуже, на её обратную сторону? А если между планетой игрока и планетой с маркером окажется ещё одна? Маркер должен всегда быть на горизонте и менять своё положение с изменением точки обзора.

При этом здания в этот момент вообще не существует, поскольку оно, как и всё остальное, генерируется процедурно. Так что движок ищет ближайшее строение необходимого типа, для чего нужно начать генерировать местоположение зданий, что тоже сложный процесс, поэтому включается многопоточность.

Затем нужно сгенерировать основы ландшафта, на котором стоят эти здания. И это тоже сложный процесс, так что приходится вводить дополнительные переменные. Потом нужно учитывать, может ли здание находиться в этом месте — может быть, оно под водой или на слишком крутом склоне. Словом, процесс очень сложный, а ведь речь только о маркерах и зданиях.

Но Мюррею нравится работать со всеми этими проблемами. No Man’s Sky стала идеальным полем экспериментов для человека, которому наскучила стандартная разработка движков.

No Man’s Sky — одновременно большая и маленькая игра. Во время релиза объём билда, скачиваемого в Steam, составлял всего два гигабайта, полтора из которых ушло на аудиоматериалы. Движок, отвечающий за весь мир игры, «весил» примерно 300 мегабайт. Отчасти из-за низкого объёма исходных файлов Мюррей считает процедурную генерацию очень перспективной сферой для веб-игр.

Проект разрабатывала небольшая команда — в среднем над ним единовременно работало шесть человек.

Сначала генерируется шум, то есть части ландшафта, население планет и так далее. Затем это превращается в воксели и полигонизируется, после чего рендерится и обсчитывается физически.

Главной проблемой (и одновременно — целью) было создание разнообразных миров, которые удивляли бы людей и даже своего создателя, но были бы играбельными и предсказуемыми — нужно было понимать, сколько памяти они будут занимать.

Впервые Мюррей попытался решить эту проблему, скопировав Minecraft (популярный подход в то время). Он использовал тот же метод генерации мира: трилинейное фильтрованное поле шума Перлина низкой плотности.

Поскольку разработчик хотел, чтобы игра выглядела реалистично, этот способ в итоге не подошёл — он хорошо подходит только генерации миров из кубиков.

Источник статьи: http://dtf.ru/gamedev/6874-shum-perlina-matematika-i-generaciya-mira-no-man-s-sky

Пишем настоящий шум Перлина

По поисковому запросу шум перлина сразу попадается этот перевод на Хабре. Как справедливо заметили в комментариях к публикации, речь идёт вовсе не о шуме Перлина. Возможно, автор перевода и сам был не в курсе.

Чем выгодно отличается шум Перлина, легко можно заметить, если сравнить картинки.

Обычный шум (из той самой статьи):

Шум Перлина:

И увеличением количества октав первую картинку ко второй никак не приблизишь. Я не буду описывать достоинства шума Перлина и область его применения (потому что статья о программировании, а не о применении), а постараюсь объяснить как он реализован. Думаю, это будет полезно многим программистам, ведь хакерские исходники Кена Перлина мало объясняют даже при наличии комментариев.

Отступление

Поразительно, но судя по отзывам в личку и в комментарии оказалось, что далеко не все способны видеть вообще какую-либо разницу между простым сглаженным шумом в градациях серого и шумом Перлина. Но, наверное, из-за этого парадокса и появилась и поимела популярность та самая статья.

Попробую дать наводку:
первая картинка состоит из явно выраженных пикселей (увеличенных) разных оттенков серого:

Вторая же (шум Перлина) выглядит как черно-белые размытые черви.

Вот что получается после несложных операций в графическом редакторе (поиск границ, инвертирование, постеризация):
Перлин:

Картинка из статьи (применены точно те же операции):

Да, во фрактальном шуме, если октав много, то понять, что там лежит в оригинале — Перлин или нет уже и правда сложно. Но это ведь не повод назвать фрактальный шум Шумом Перлина.
На этом закончу с описанием разницы.
Конец отступления.

Рассмотрим двухмерный вариант. Пока напишем только класс-заготовку. Входящие данные — двухмерный вектор или два числа с плавающей точкой: x, y.

Возвращаемое значение — число от -1.0 до 1.0:

Пару слов об интерполяции

Идея обычного сглаженного шума в том, что есть дискретная сетка псевдослучайных значений, и для запрашиваемой точки происходит интерполяция между узлами сетки (чем ближе точка к какому-нибудь узлу сетки, тем больше его значение соответствует значению узла).

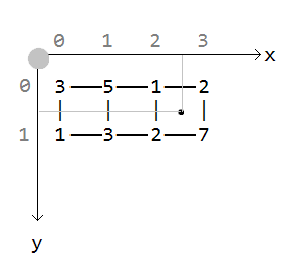
Здесь в третьем условном квадрате точка в самом центре после интерполяции будет иметь значение 3:

Рассмотрим детальнее как там получается тройка. Координаты точки:
x:2.5,
y:0.5

Целочисленные координаты точки (верхний левый угол квадрата):
x:2,
y:0

получаются округлением в меньшую сторону (функция floor).

Локальные координаты точки внутри квадрата получаются вычитанием:
x = 2.5 – 2 = 0.5,
y = 0.5 – 0 = 0.5

Берём значение левого верхнего угла квадрата (1) и верхнего правого (2). Интерполируем верхнюю грань используя локальную координату x (0.5). Линейная интерполяция выглядит так:

Берём значение левого нижнего угла квадрата (2) и нижнего правого (7). Интерполируем нижнюю грань используя всё ту же локальную координату x (0.5).
Результаты:
верхняя: 1.5
нижняя: 4.5

Теперь осталась интерполяция верхней и нижней с использованием локальной координаты y (тоже 0.5):
1.5 * 0.5 + 4.5 * (1 – 0.5) = 3

Билинейная интерполяция самая простая но и результат не самый привлекательный.

Другие варианты интерполяции подразумевают модифицирование локальной координаты (параметра t) перед интерполяцией. Получаются более плавные переходы возле граничных значений (0 и 1).

В шуме Перлина задействован первый вариант, он даёт достаточно сильное искривление.

Главная идея и отличие шума Перлина

Всё очень просто:
1. В узлах сетки — псевдослучайные вектора (двухмерные для двухмерного шума, трехмерные для трехмерного и так далее), а не псевдослучайные числа.
2. Интерполируем между скалярными произведениями a) векторов от вершин квадрата до точки внутри квадрата (куба в трехмерном варианте) и b) псевдослучайных векторов (при описании шума Перлина их называют градиентными векторами).

В своём улучшенном варианте шума Кен Перлин использует всего 12 градиентных векторов. Для двухмерного варианта требуется всего 4 — по количеству граней (у квадрата их 4). Вектора направлены (условно из центра куба/квадрата) в сторону каждой из граней и не нормализованы.

Итак, каждому узлу сетки соответствует один из четырёх векторов. Пусть вектор у нас будет массивом float-ов.

Реализация

Нам понадобится скалярное произведение векторов:

В качестве бонуса:

И последнее — использование таблицы со случайными числами. В коде Кена Перлина такая таблица прописана вручную и достаются оттуда значения совсем по-другому. Здесь можно экспериментировать и от этого немало зависит равномерность шума и отсутствие в нём явных паттернов.

& 3 здесь обрезает любое int32 число до 3, читайте об операции AND на википедии
Операция типа % 3 тоже сработала бы, но намного медленней.

Результат:

Ой, у вас баннер убежал!

Читают сейчас

Редакторский дайджест

Присылаем лучшие статьи раз в месяц

Скоро на этот адрес придет письмо. Подтвердите подписку, если всё в силе.

Похожие публикации

Нечёткий мир шума Перлина

Шум Перлина

Шум Перлина (Perlin Noise)

Вакансии

AdBlock похитил этот баннер, но баннеры не зубы — отрастут

Минуточку внимания

Комментарии 18

Вроде должно быть

Я не буду описывать достоинства шума Перлина и область его применения, а постараюсь объяснить как он реализован.

Были другие статьи про генерацию ландшафта, например, не хотелось повторяться.
В майнкрафто-подобной игре, например, если на лету использовать фрактальный шум это сильно ударит по скорости кадров. А если еще и взять вот такой шум, где куча операций сглаживания на одну октаву так тем более.
Сам же сырой Перлин уже хорош для простых холмов.

Кстати, обычный пиксельный шум выглядит намного приличнее, если использовать 2 слоя: второй слой, не меняя масштаб, повернуть на 45 градусов:

Очень просто реализовывается:

Но Перлин2д всё равно чуть быстрее и плавнее вдоль тела «червя».

получаются округлением в сторону 0 (функция floor).

Действительно, забыл про отрицательные числа. Исправил.

Как справедливо заметили в комментариях к публикации, речь идёт вовсе не о шуме Перлина. Возможно, автор перевода и сам был не в курсе.

Автор перевёл (коряво, но перевёл а не написал) статью Perlin Noise, которая называется кто бы мог подумать — так как называется и которая попадается в выдаче google первой (до появления этих двух и статьи на вики) с достаточно подробным описанием, на которую ссылается довольно много статей в первую очередь на англоязычных ресурсах.

vs
как миниму не корректное и взято явно для «показательной непригодности варианта слева», однако если взять первую октаву другого размера например:

то различие не такое уж заметное.

Кроме того, назвав «обычным шумом из той самой статьи» одну октаву со сглаживанием, вы
видимо не дочитали или разнося в пух и прах не увидели что шумом названо нечто другое:

Поправьте, если не прав: псевдослучайные числа — это псевдослучайные вектора кто бы мог подумать в одномерном пространстве
и возможно взяты для упрощения понимания (что задумал автор можно только догадываться). И собственно способ получения этих векторов и является настройкой параметров генерации, можно получать на ходу — дабы не хранить в памяти там где это критично, можно загружать из… да хоть из текстуры это уже не важно, важен принцип.

Соответственно и принцип работы тоже варьируется.

Как итог: «та самая статья», фу какая мерзкая, была написана переведена из академического интереса, и как верно замечено в комментариях, код не достаточно эффективен, но при этом даёт представление как сгенерировать некий шум, который кто то назвал шумом перлина, однако чрезвычайно на него похож когда это надо и не похож когда это удобно О_о.

И кстати «фрактальный шум на базе Перлина»(из комментария выше), ну очень похож на то что названо шумом перлина в «той самой статье», даже больше чем у вас чего бы О_о.

как миниму не корректное и взято явно для «показательной непригодности варианта слева», однако если взять первую октаву другого размера например:
то различие не такое уж заметное.

Кроме того, назвав «обычным шумом из той самой статьи» одну октаву со сглаживанием, вы
видимо не дочитали или разнося в пух и прах не увидели что шумом названо нечто другое:

Поправьте, если не прав: псевдослучайные числа — это псевдослучайные вектора кто бы мог подумать в одномерном пространстве
и возможно взяты для упрощения понимания (что задумал автор можно только догадываться).

Как итог: «та самая статья», фу какая мерзкая, была написана переведена из академического интереса, и как верно замечено в комментариях, код не достаточно эффективен, но при этом даёт представление как сгенерировать некий шум, который кто то назвал шумом перлина, однако чрезвычайно на него похож когда это надо и не похож когда это удобно О_о.

И кстати «фрактальный шум на базе Перлина»(из комментария выше), ну очень похож на то что названо шумом перлина в «той самой статье», даже больше чем у вас чего бы О_о.

Сначала попробую убедиться в том что все всё поняли: я прямо не называю шумом перлина ни то что описано в первой статье ни то что во второй, является оно таковым или нет.

теперь по существу:
речь про сравнение, сравните размерность сравниваемого в статье, речь идёт именно о размерности. можно было с таким же успехом взять монохромное изображение изображение 2х2 px увеличить размерность замылить его и сказать: «оно не похоже на шум перлина чего бы мы не сделали», если приведённую в моём коментарии октаву интерполировать с большим радиусом сглаживания(фактически поменять коэффициенты или способ интерполяции) то получить можно очень даже похожую картинку, а про обведённое тут никто не спорит что это не шум перлина, речь про явное различие сравниваемого

Для двумерного шума Перлина нужны именно двумерные вектора

1. В узлах сетки — псевдослучайные вектора (двухмерные для двухмерного шума, трехмерные для трехмерного и так далее), а не псевдослучайные числа.

чем в данном описании псевдослучайные числа отличаются от одномерных векторов, раз уж упоминаются более чем двумерные или принято только в одну сторону размерность менять?

Опять же, я не упоминал двумерный шум перлина.

теперь по существу:
речь про сравнение, сравните размерность сравниваемого в статье

Кроме того, назвав «обычным шумом из той самой статьи» одну октаву со сглаживанием, вы
видимо не дочитали или разнося в пух и прах не увидели что шумом названо нечто другое: (и тут картинка фрактального шума)

чем в данном описании псевдослучайные числа отличаются от одномерных векторов, раз уж упоминаются более чем двумерные или принято только в одну сторону размерность менять?

спасибо конечно, но к сожалению через чур злоупотребил переводчиком, и поторопившись не вычитал хорошенько, из-за чего обоснованно «получил по ушам» в комментариях.

Ваша статья (хоть и с ошибкой в названии шума) — гораздо ближе лежит к практике, чем эта. Шум описанный у вас применяется чаще, т.к. он дешевле и проще реализуется. Однако знать разницу между нормальным шумом и шумом Перлина все таки полезно.

Дополнение:
После обновления статьи добавились картинки «червячков». Не совсем удачные, имхо. Эту

картинку стоило бы увеличить с бикубической интерполяцией, чтобы не было сильно выраженной «квадратности». Тогда на этой картинке тоже были бы «червячки», но! на этой картинке кроме червячков стали бы образовываться острова, у червячков были бы утолщения. К сожалению инструмента под рукой сейчас нет, чтобы создать такую картинку.

Источник статьи: http://habr.com/ru/post/265775/