Решение задачи про грядки

ОГЭ 2020 задания 1 – 5 (теплица)

Прочитайте внимательно текст и выполните залдания 1 — 5.

Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент.

Задание 1 (ОГЭ 2020)

Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?

Решение: Длина теплицы составляет 4 м = 400 см. Рассчитаем количество дуг для теплицы, соблюдая условие: расстояние между соседними дугами меньше или равно 60 см. Разделим 400 на 60. Получится 6 дуг и в остатке 40 см. Учитывая две крайние дуги, получается:6 + 2 = 8 (дуг).

Ответ: 8.

Задание 2 (ОГЭ 2020)

Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продается в упаковках по 6 штук?

Решение: Из условия задачи имеем, что грядок в теплице планируется 3. Дорожек будет 2. Длина дорожки совпадает с длиной теплицы, то есть 4 м = 400 см. Ширина дорожки – 40 см. Найдем площадь двух дорожек. 2 * 40 * 400 = 32000 (кв. см).

Площадь одной плитки: 20 * 20 = 400 (кв. см).

32000 : 400 = 80 (штук) плиток нужно купить для двух дорожек.

80 : 6 = 13 (остаток 2).

Понадобится 13 + 1 = 14 упаковок плитки.

Ответ: 14.

Задание 3 (ОГЭ 2020)

Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.

Решение:

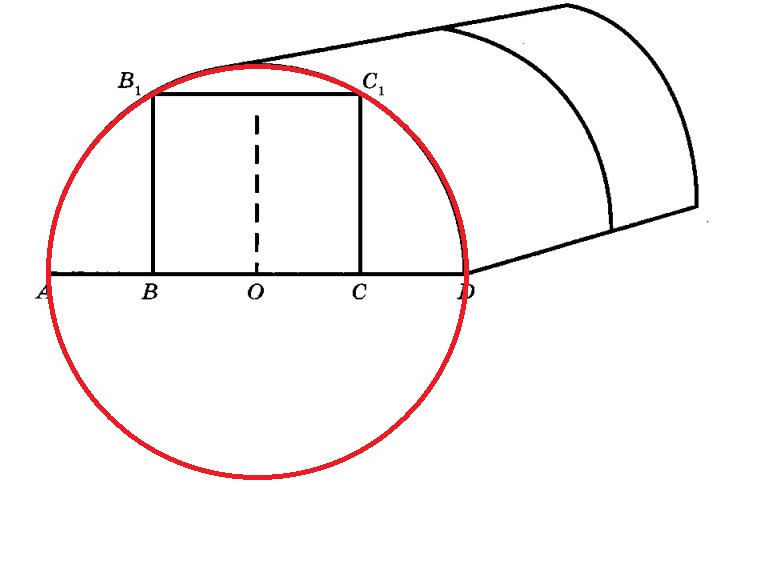
Дуги для теплицы имеют форму полуокружности. Чтобы найти ширину теплицы, нужно достроить окружность и найти радиус окружности OD.

Ширина теплицы AD является диаметром окружности. AD = 2 * OD.

Длина дуги теплицы равна 5 м и вычисляется по формуле П * OD (это длина полуокружности).

OD = 5 : 3,14 = 1,6 (м).

AD = 2 * OD = 2 * 1,6 = 3,2 (м).

Ответ: 3,2.

Задание 4 (ОГЭ 2020)

Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятых.

Решение: Ширина теплицы 3,2 м = 320 см. В теплице есть 2 дорожки по 40 см и три грядки. Пусть ширина узкой грядки х см, тогда широкой грядки – 2х см.

Составим уравнение 2х + х + х + 2 * 40 = 320 и решим его.

х = 60 (см) – ширина узкой грядки.

Найдем ширину центральной грядки (широкой). 2х = 2 * 60 = 120 (см).

Ответ: 120.

Задание 5 (ОГЭ 2020)

Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.

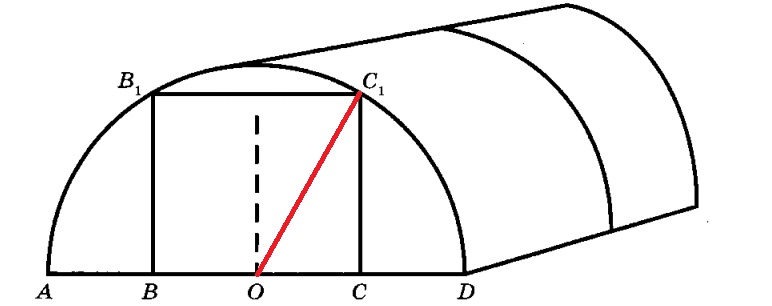
Чтобы найти высоту входа в теплицу,нужно рассмотреть прямоуголный треугольник OC1A. Применив теорему Пифагора, вычислим высоту CC1 теплицы.

По условию AB = BO = OC = CD = 320 см : 4 = 80 см.

ОС1 = OD = 160 см – радиусы.

По теореме Пифагора имеем: СС1 = 80√3 см = 136 см.

Ответ: 136.

Подробный ОГЭ 2020 — земледелец устраивает на склонах гор терассы — задания 1 — 5.

Источник статьи: http://mathembox.xyz/2020/03/09/ogje-2020-zadanija-1-5-teplica/

Решение задачи про грядки

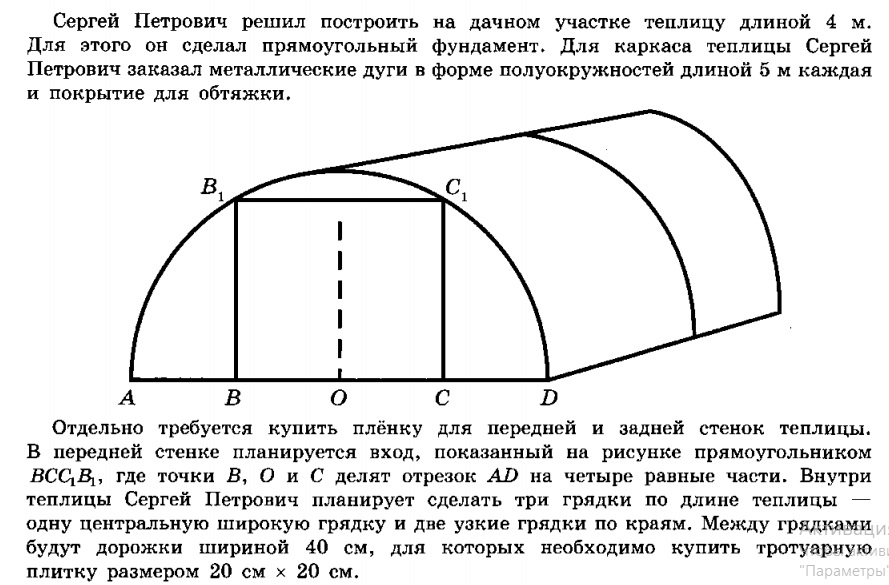
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.

Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником BCC1B1, где точки B, O и C делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.

Задание 1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?

Вся длина теплицы составляет 4 м = 400 см. Разделим эту длину на 60 см и округлим результат до ближайшего наибольшего целого, получим:

то есть, нужно заказать 7 дуг + 1 первая дуга = 8 дуг.

Задание 2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?

В теплице 3 грядки, между которыми будут дорожки, т.е. всего две дорожки. Длина каждой дорожки равна длине теплицы – 400 см, а ширина – 40 см. Площадь одной дорожки 400∙40 = 16000 см2, а двух – 2∙16000 = 32000 см2. Тротуарная плитка имеет размеры 20х20 см с площадью 400 см2. Следовательно, на дорожки необходимо

32000:400 = 80 плиток

Так как плитки продаются в упаковках по 6 штук, то необходимо купить

упаковок

(здесь — округление до ближайшего наибольшего целого).

Задание 3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.

Ширина теплицы определяется диаметром полуокружности длиной 5 метров. Для вычисления радиуса такой полуокружности можно воспользоваться формулой длины окружности . Для полуокружности она будет выглядеть так: , откуда

и ширина теплицы, равна:

м

Задание 4. Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.

Условно представим теплицу с грядками: две по краям с шириной x см и одна центральная с шириной в 2 раза больше – 2x см. Между ними дорожки шириной 40 см.

Учитывая, что вся ширина теплицы примерно 3,2 м = 320 см, получаем уравнение:

То есть, ширина центральной грядки примерно 120 см.

Задание 5. Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.

Так как по условию задания точки B, O и C делят отрезок AD на четыре равные части. Учитывая, что AD=320 см, то AB = 320:4 = 80 см.

Учитывая, что радиус изображенной окружности R=160 см, то можно записать равенство:

Тогда, высоту входа можно найти по формуле:

То есть, высота входа примерно равна 139 см.

Источник статьи: http://self-edu.ru/oge2020_36.php?id=5_1

Задача-нерешайка. Только единицы смогут решить эту задачу про начинающих дачников

Условия задачи:

Молодая семья – муж и жена, купили дачу и решили вскопать грядки.

Под капусту решили делать грядки побольше, а под огурцы — поменьше.

Муж стал копать грядку под капусту, а жена под огурцы.

В итоге они вскопали свои грядки одновременно.

После обеда решили сделать наоборот — муж вскопал грядку под огурцы, а жена под капусту.

В итоге муж закончил работу за 48 минут, а жена за 1 час 15 минут.

Производительность труда у каждого была постоянна на протяжении всего дня.

Сколько времени начинающие дачники потратили на свои первые грядки?

Правильное решение задачи для самопроверки внизу страницы.

Предложите в комментариях свой вариант решения этой задачи.

Решение задачи:

Обозначим время за которое муж с женой вскопали свои первые грядки за х минут.

Если бы муж вскопал все четыре грядки самостоятельно, то он бы потратил на это х + 48 минут.

А если бы это сделала жена, то она потратила бы на это х + 75 минут.

Получается, что в минуту муж вскапывал 1 / (х + 48) часть четырех грядок.

А жена вскапывала за одну минуту 1 / (х + 75) часть этих грядок.

Ну, а поскольку вместе за минуту они проделывали 1 / х всей работы, то мы можем составить уравнение:

Ответ: свои первые грядки муж с женой вскопали за один час.

Подписывайтесь на канал, ставьте лайк!

Источник статьи: http://zen.yandex.ru/media/matematik/zadachanereshaika-tolko-edinicy-smogut-reshit-etu-zadachu-pro-nachinaiuscih-dachnikov-5c8a6352211f3d00b3fddae1

Решение задачи про грядки

Сергей Петрович решил построить на дачном участке теплицу длиной 6 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 6 м каждая и покрытие для обтяжки.

Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником ВСС1В1, где точки B, O и C делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 60 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.

Задание 1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 80 см?

Вся длина теплицы составляет 6 м = 600 см. Разделим эту длину на 80 см и округлим результат до ближайшего наибольшего целого, получим:

то есть, нужно заказать 8 дуг + 1 первая дуга = 9 дуг.

Задание 2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 10 штук?

В теплице 3 грядки, между которыми будут дорожки, т.е. всего две дорожки. Длина каждой дорожки равна длине теплицы – 600 см, а ширина – 60 см. Площадь одной дорожки 600∙60 = 36000 см2, а двух – 2∙36000 = 72000 см2. Тротуарная плитка имеет размеры 20х20 см с площадью 400 см2. Следовательно, на дорожки необходимо

72000:400 = 180 плиток

Так как плитки продаются в упаковках по 10 штук, то необходимо купить

180:10 = 18 упаковок

Задание 3. Найдите ширину входа в теплицу. Ответ дайте в метрах с точностью до десятых.

Ширина теплицы определяется диаметром полуокружности длиной 6 метров. Для вычисления радиуса такой полуокружности можно воспользоваться формулой длины окружности . Для полуокружности она будет выглядеть так: , откуда

и ширина теплицы, равна:

м

Так как AB=BO=OC=CD по условию текста задания, то ширина входа

м

Задание 4. Найдите ширину центральной грядки, если ширина узкой грядки относится к ширине центральной грядки как 3:4. Ответ дайте в сантиметрах с точностью до целых.

Условно представим теплицу с грядками: две по краям с шириной см и одна центральная с шириной x см. Между ними дорожки шириной 60 см.

Учитывая, что вся ширина теплицы примерно 3,8 м = 380 см, получаем уравнение:

То есть, ширина центральной грядки примерно 104 см.

Задание 5. Сколько процентов составляет площадь, отведённая под грядки, от площади всего участка, отведённого под теплицу? Ответ округлите до целых.

Площадь, занимаемая грядками, равна:

см2,

а площадь всей теплицы:

см2.

Отношение этих площадей, равно:

,

то есть, грядки занимают примерно 68% от площади всей теплицы.

Источник статьи: http://self-edu.ru/oge2020_36.php?id=33_1

Как легко решить ОГЭ? Задачи с теплицей

Задача о теплице, входит в первые пять заданий огэ по математике, и является практико-ориентированной задачей. Сложность данной задачи заключается в том, что в 5 задании требуется найти приближенное значение арифметического квадратного корня, и попасть в интервал ответов.

Вот текст задачи:

По этому тексту, нужно ответить на 5 вопросов.

1) Какое наименьшее количество дуг, нужно нужно заказать, чтобы расстояние между соседними дугами было не более 70 см.

Из первого предложения текста задачи, мы узнаем, что длина теплицы составляет 6 метров. Поэтому, первым делом находим количество интервалов, между дугами.

Теперь найдем, сколько будет дуг. Количество дуг = количество интервалов +1 = 9+1 = 10 дуг. Ответ 10

2) Сколько упаковок плитки необходимо купить для дорожек между грядками, она продается в упаковках по 14 штук?

Для этого вопроса, информация в тексте задачи дана в последнем предложении «Между грядками будут дорожки шириной 50 см, для которых необходимо купить тротуарную плитку размером 25х25»

Поскольку у нас ширина дорожки 50 см, а ширина плитки 25 см, то в ширину дорожки можно уложить 2 плитки. Длина у нас 6 метров, что составляет 600 см, поэтому в длину уместится 24 плитки. Тогда во всей дорожке будет 48 плитки. а в двух дорожках 96 штук.

Расчет количества упаковок приведен ниже.

3) Найдите ширину теплицы. Ответ дайте в метрах до сотых.

Ширина теплицы — это отрезок АD. Поскольку теплица состоит из дуг, то АD- это диаметр окружности.

Диаметр окружности связан с длиной окружности следующей формулой:

В этой формуле, L-длина окружности, D- диаметр окружности, «пи»=3,14

Длину окружности, найдем из следующей информации: » . металлические дуги в форме полуокружности длиной 5,53 метра. «

Поскольку известна длина полуокружности — 5,53 м, то длина окружности равна:

Из этих расчетов получаем, что ширина теплицы (с округлением до сотых) равна 3,52

4) Найти ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте до десятков, с точностью до десятков.

Для ответе на этот вопрос, сделаем схематический чертеж:

В этой задаче, за Х взяли ширину узкой грядки. Тогда широкая грядка будет 2Х. В задаче у нас две дорожки, что показано на схеме, которые составляю по 50 см.

По схеме составим уравнение:

Поскольку в задаче написано условие, что результат нужно округлить до десятков, поэтому получаем ответ 130.

5)Найти высоту входа в теплицу. Ответ дайте в сантиметрах.

Для расчета высоты теплицы, нам необходимо сделать дополнительные построения. Проводим ОС1. Получаем прямоугольный треугольник, ОС1С. Дальше по теореме Пифагора, выразим СС1. Для этой задачи, покажу три разных варианта завершения задачи.

При таком решении, получаем неизвлекаемый корень из 3. На экзамене, хорошо, что хоть кто нибудь вспомнит, что примерно он равен 1,7. Но такого значения не достаточно, поскольку мы получаем, что высота входа равна 149,6. Но такой ответ нас не устраивает, поскольку верный ответ находится в интервале от 150-160 см

Поэтому в этой задаче, чем точнее ответ, тем больше вероятность, что ответ будет не верный, не попадете в интервал правильного ответа.

В этом варианте, мы не будем раскладывать числа до последнего множителя, а будем раскладывать число на множители таким образом, что бы получилось приближенное число из таблицы квадратов. В этом случае, 23232 можно поделить на 16 (признак делимости на 4, если последние два числа делятся на 4)

Как видите, оба ответа, 152 и 156 подходят под наш интервал решения.

Третий вариант: воспользуемся канадской формулой вычисления приближенного значения квадратного корян.

Как видим, эту формулу. так же можно использовать для решения этой задачи.

Спасибо, что прочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.

Источник статьи: http://zen.yandex.ru/media/id/5ff958485d3c8f7ab915e8c3/kak-legko-reshit-oge-zadachi-s-teplicei-600b02ddcdf9ab055a56dd95