Некоторые определения теории графов
Связные графы , в которых существует одна и только одна цепь, соединяющая каждую пару вершин, называются деревьями . Дерево можно определить и как связный граф , не содержащий циклов.
Пример. Кубок по настольному теннису разыгрывается по олимпийской системе. Встречи проводятся без «ничьих». К очередному туру допускается только победившая в предыдущем туре команда . Проигравшие команды выбывают из игры. Для завоевания кубка команда должна победить во всех турах. На участие в розыгрыше кубка поданы заявки от команд.
Схема проведения игр изображается графом
Вершины нижнего «яруса» дерева интерпретируем как команды, участвующие в розыгрыше кубка, вершины второго снизу яруса — как команды-победительницы в 
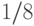
Какую информацию можно получить с помощью этого дерева?
Непосредственно с него считываются:
- Число всех участников розыгрыша кубка (число вершин нижнего «яруса»).
- Число этапов проведения розыгрыша (число «ярусов» из вершин в дереве, не считая нижнего).
- Число команд, участвующих в
финала, в
финала, в
финала (число вершин, соответственно, в четвертом сверху ярусе, в третьем сверху ярусе, во втором сверху ярусе).
- Число матчей, которые придется сыграть командам для выявления обладателя кубка (число вершин в графе без нижнего «яруса»). Хотя это число легко определяется и без дерева. (В каждом матче выбывает одна команда. Для того чтобы была выявлена команда-победительница, остальные должны выбыть из соревнования. Поэтому число матчей равно числу команд без одной, а именно
).
Удобно считать, что граф , состоящий из одной изолированной вершины, тоже является деревом. Для каждой пары вершин дерева существует единственный соединяющий их путь . Лесом называется несвязный граф , представляющий объединение деревьев. Всякое ребро в дереве и в лесе является мостом (признак 3).
Изображен лес , состоящий из четырех компонент , каждая из которых является деревом.
Заметим, что по определению деревья и леса являются простыми графами. По многим показателям дерево представляет собой простейший нетривиальный тип графа.
Известно, что в связном графе 


В общем случае обозначим через 









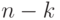
Теорема 2.1 Дерево с 

Доказательство Для того чтобы из одного дерева 









Источник
Некоторые определения теории графов
Связные графы , в которых существует одна и только одна цепь, соединяющая каждую пару вершин, называются деревьями . Дерево можно определить и как связный граф , не содержащий циклов.
Пример. Кубок по настольному теннису разыгрывается по олимпийской системе. Встречи проводятся без «ничьих». К очередному туру допускается только победившая в предыдущем туре команда . Проигравшие команды выбывают из игры. Для завоевания кубка команда должна победить во всех турах. На участие в розыгрыше кубка поданы заявки от команд.
Схема проведения игр изображается графом
Вершины нижнего «яруса» дерева интерпретируем как команды, участвующие в розыгрыше кубка, вершины второго снизу яруса — как команды-победительницы в 
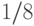
Какую информацию можно получить с помощью этого дерева?
Непосредственно с него считываются:
- Число всех участников розыгрыша кубка (число вершин нижнего «яруса»).
- Число этапов проведения розыгрыша (число «ярусов» из вершин в дереве, не считая нижнего).
- Число команд, участвующих в
финала, в
финала, в
финала (число вершин, соответственно, в четвертом сверху ярусе, в третьем сверху ярусе, во втором сверху ярусе).
- Число матчей, которые придется сыграть командам для выявления обладателя кубка (число вершин в графе без нижнего «яруса»). Хотя это число легко определяется и без дерева. (В каждом матче выбывает одна команда. Для того чтобы была выявлена команда-победительница, остальные должны выбыть из соревнования. Поэтому число матчей равно числу команд без одной, а именно
).
Удобно считать, что граф , состоящий из одной изолированной вершины, тоже является деревом. Для каждой пары вершин дерева существует единственный соединяющий их путь . Лесом называется несвязный граф , представляющий объединение деревьев. Всякое ребро в дереве и в лесе является мостом (признак 3).
Изображен лес , состоящий из четырех компонент , каждая из которых является деревом.
Заметим, что по определению деревья и леса являются простыми графами. По многим показателям дерево представляет собой простейший нетривиальный тип графа.
Известно, что в связном графе 


В общем случае обозначим через 









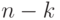
Теорема 2.1 Дерево с 

Доказательство Для того чтобы из одного дерева 









Источник
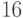
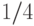 финала, в
финала, в 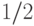 финала (число вершин, соответственно, в четвертом сверху ярусе, в третьем сверху ярусе, во втором сверху ярусе).
финала (число вершин, соответственно, в четвертом сверху ярусе, в третьем сверху ярусе, во втором сверху ярусе).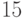 ).
).