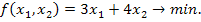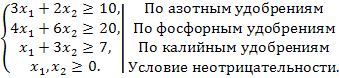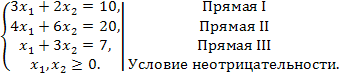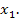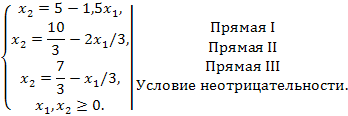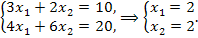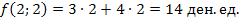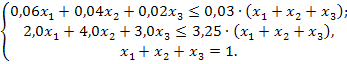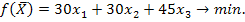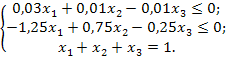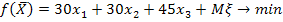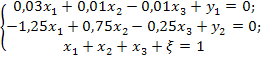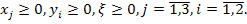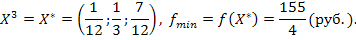Задачи оптимизации
Задача № 1. Решить графическим методом типовую задачу оптимизации.
Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений, а в улучшенный – 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений. Известно, что для некоторого газона требуется по меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений. Обычный набор стоит 3 ден. ед., а улучшенный – 4 ден. ед. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум и почему?
1. Введем переменные:
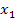
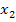
2. Зададим целевую функцию. Задача на минимизацию затрат. Запишем уравнение, описывающее затраты
Найдем решение сформированной задачи, используя ее геометрическую интерпретацию. Сначала определим область допустимых решений. Для этого в неравенствах системы ограничений знаки неравенств заменим на знаки точных равенств, и найдем соответствующие прямые:
Выразим 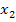
Для построения прямой достаточно двух точек, найдем их координаты:
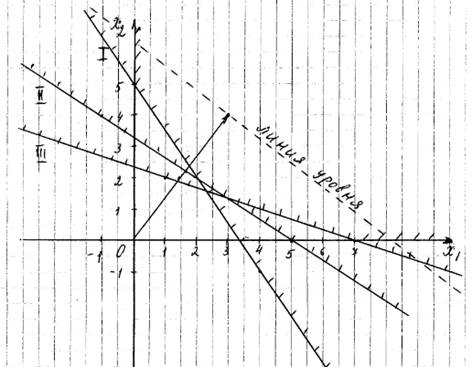
Эти прямые изображены на рисунке 1. Условие неотрицательности показывает, что искомая область располагается в первой четверти.
Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой – нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли ее координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае – другая полуплоскость.
Рисунок 1. Графический метод решения
На рисунке 1, область допустимых решений не ограничена и отмечена штрихом. Координаты любой точки, принадлежащей этой области, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую области допустимых решений, в которой целевая функция принимает минимальное значение. Чтобы найти указанную точку, построим вектор 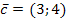
Так как задача на минимум, то линию уровня будем двигать по направлению вектора. Первая точка касания и будет оптимальным решением. Координаты этой точки и определяют оптимальные количества обычных и улучшенных наборов удобрений, при которых затраты являются минимальными.
В данном примере это точка пересечения прямых I и 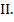
Следовательно, если фирма купит 2 обычных и 2 улучшенных набора удобрений, то минимальные затраты составят
Если данную задачу решать на максимум, то линия уровня будет сдвигаться вправо до бесконечности (так область решений не ограничена). Таким образом, конечного решения не будет.
Задача № 2. Предложить оптимальное управленческое решение в следующих типовых хозяйственных ситуациях.
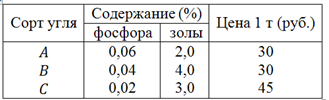
Металлургическому заводу требуется уголь с содержанием фосфора не более 0,03% и с долей зольных примесей не более 3,25%. Завод закупает три сорта угля 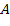
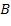
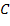
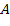
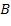
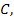
Введем следующие обозначения: 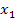
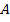
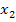
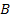
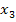
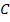
Целевая функция задачи:
Таким образом, ЭММ задачи имеет вид:
Решим данную задачу симплекс-методом. Преобразуем исходную модель. В ограничения типа 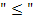
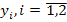
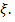
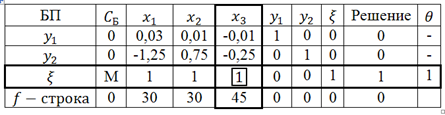
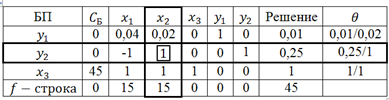
Заполним первую симплекс-таблицу.
В 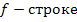
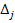
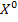
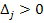
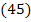
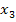
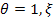
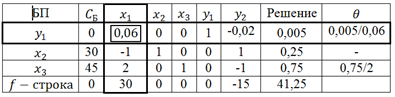
В 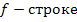
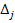
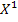
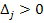
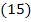
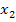
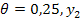
В 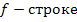
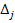
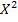
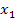
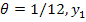
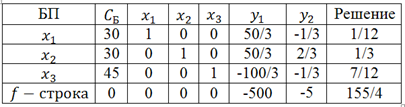
В 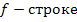
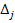
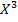
Полученное оптимальное решение означает, что для получения 1 т угля необходимо взять 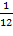
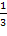
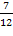
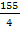
Задача № 3. Провести моделирование и решить специальную задачу линейного программирования.
Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у. е.) на перевозку 1тонны песка с карьеров на ремонтные участки.
Числовые данные для решения содержатся ниже в Матрице планирования. Требуется:
1) Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.
2) Что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ?; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами?
Источник статьи: http://matica.org.ua/primery/primery/zadachi-optimizatcii
Задание 2. Фирма выпускает два вида комплексных удобрений для газонов в упаковке – обычное и улучшенное
Фирма выпускает два вида комплексных удобрений для газонов в упаковке – обычное и улучшенное. Обычное удобрение стоит 3 дн. ед./уп. и включает 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений. Улучшенное удобрение стоит 4 ден. ед./уп. и включает 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений.
Для подкормки некоторого газона требуется по меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений.
Определите, сколько и каких удобрений нужно купить, чтобы обеспечить эффективное питание растений и минимизировать стоимость покупки.
Постройте экономико-математическую модель задачи, дайте необходимые комментарии к ее элементам и получите решение графическим методом. Что произойдет, если решать задачу на максимум, и почему.
Осуществите проверку правильности решения с помощью средств MS Excel (надстройка Поиск решения).
Обозначим через х1 и х2, соответственно, количество обычных и улучшенных наборов удобрений.
Составим целевую функцию и систему ограничений.
min
Прямые ограничения означают, что область решений будет лежать в первой четверти декартовой системы координат. По ограничениям строим область всех допустимых решений.
Определим множество решений первого неравенства. Оно состоит из решения уравнения и строгого неравенства. Решением уравнения служат точки прямой 3х1 + 2х2 –10 = 0. Построим прямую по двум точкам: (0; 5) и (2; 2). На рис. 2.1 обозначим ее цифрой I.
Определим множество решений второго неравенства. Построим линию по точкам: (5;0) и (2;2). На рис. 2.1 обозначим ее цифрой II.
Определим множество решений третьего неравенства. Построим линию по точкам: (7;0) и (1;2). На рис. 2.1 обозначим ее цифрой III.
Пересечением всех плоскостей является неограниченная область ABCDEF (рис. 2.1).
Рис. 2.1. Графическое решение задачи
Для определения направления движения к оптимуму построим вектор-градиент, соединив его вершину ∆(3;4) с началом координат.
Построим линию уровня 3x + 4y = 0 по точкам: (0;0) и (4;-3). Эта линия будет перпендикулярна вектору-градиенту.
При минимизации целевой функции необходимо перемещать линию уровня в направлении, противоположном вектору-градиенту. В данном примере, первое касание прямой области допустимых решений произойдет в точке С (2;2). В точке С значение функции будет наименьшим:
f(min) = f(2;2) = 3 * 2 + 4 * 2 = 14 ден. ед.
Таким образом, чтобы минимизировать стоимость удобрений, необходимо купить 2 обычных набора удобрений и 2 улучшенных набора удобрений. При этом минимальные затраты на покупку удобрений составят 14 ден. ед.
Построенная область допустимых решений не ограничена сверху, следовательно, если задачу решать на максимум, то f(max) = ∞, т.е. не имеет конечного оптимума, так как область допустимых значений не ограничена сверху.
Проведем проверку правильности решения задачи с помощью средств MS Excel (надстройка Поиск решения).
Подготовим форму и введем в нее данные (рис. 2.2).
Рис. 2.2. Исходные данные
Введем зависимость для целевой функции (ЦФ) с помощью математической функции СУММПРОИЗВ(). В строке «Массив1» вводим C3:D3; в строке «Массив 2» – С4:D4. Нажимаем ОК (рис. 2.3).
Рис. 2.3. Зависимость для целевой функции
Далее аналогично введем с помощью математической функции СУММАПРОИЗВ() зависимости для всех ограничений:
— строка «Массив 1» — С3:D3; строка «Массив 2» — А7:В7;
— строка «Массив 1» — С3:D3; строка «Массив 2» — А8:В8;
— строка «Массив 1» — С3:D3; строка «Массив 2» — А:В9.
Далее для решения воспользуемся надстройкой Поиск решения.
Курсор в поле «Установить целевую ячейку», вводим адрес $F$4, вводим направление целевой функции – «минимальному значению».
Вводим адрес искомых переменных: курсор в поле «Изменяя ячейки», вводим адреса $C$3:$D$3.
Далее вводим ограничения. Курсор в поле «Добавить». В поле «Ссылка на ячейку» вводим адрес $D$7; знак ограничения «>=»; курсор в поле «Ограничение», вводится $F$7$, нажимаем «Добавить». Далее вводим второе и третье ограничение. Нажимаем «ОК».
На экране появится диалоговое окно «Поиск решения» с введенными условиями (риc. 2.4).
Рис. 2.4. Условия для решения задачи
Далее нажимаем «Параметры» в окне «Поиск решения».
Устанавливаем флажок на «Линейная модель», что обеспечивает применение симплекс-метода. Устанавливаем флажок на «Неотрицательные значения» (рис. 2.5).
Рис. 2.5. Параметры поиска решения
Далее нажимаем «ОК» в окне «Параметры поиска решения».
Затем нажимаем «Выполнить» в окне «Поиск решения».
В окне «Результаты поиска решения» переводим курсор на «Сохранить найденное решение» и «Результаты». Нажимаем «ОК».
Полученное решение означает, что максимум функции равен 14 при х1 = 2, х2 = 2 (рис. 2.6).
Рис. 2.6. Результаты поиска решения
Отчет по результатам решения задачи представлен на рис. 2.7.
Рис. 2.7. Отчет по результатам решения задачи
Источник статьи: http://studopedia.org/5-65834.html