Для поддержания навеса планируется использовать цилиндрическую колонну 1350

Репетитор по математике

Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».

Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]

Мой видеокурс подготовки к ЕГЭ (1-12 задание)

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Преимущества

Педагогический стаж

Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.

Источник статьи: http://mathlesson.ru/larin295var-ege

Репетитор по математике

Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».

Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]

Мой видеокурс подготовки к ЕГЭ (1-12 задание)

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Преимущества

Педагогический стаж

Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.

Источник статьи: http://mathlesson.ru/larin295var-ege

Тренировочные варианты «Школково». Вариант №6 от 15.04.2018

Среди \(12\,000\,000\) жителей города Москвы \(35\%\) не интересуется футболом. Среди жителей, интересующихся футболом, \(60\%\) будут смотреть по телевизору финал Чемпионата мира. Сколько жителей города Москвы будут смотреть этот матч по телевизору?

Найдем число жителей, интересующихся футболом. Если не интересуются футболом \(35\%\) , то интересуются \(100\%-35\%=65\%\) . Следовательно, нужно найти \(65\%\) от \(12\,000\,000\) : \(0,65\cdot 12\,000\,000=7\,800\,000\) человек.
Среди них \(60\%\) будут смотреть матч по телевизору:
\(0,6\cdot 7\,800\,000=4\,680\,000\) человек.

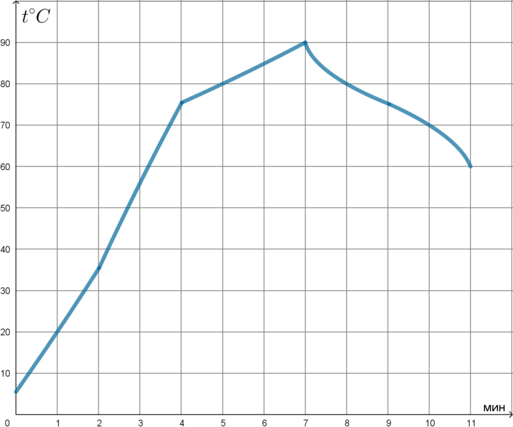
На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее с момента запуска двигателя, на оси ординат – температура двигателя в градусах Цельсия. Определите по графику, сколько минут двигатель остывал от температуры \(90^\circ C\) до температуры \(80^\circ C\) .

Остывал двигатель там, где график идет “сверху вниз” (если смотреть слева направо).
Температура составляла \(90^\circ C\) через 7 минут после начала разогрева, а \(80^\circ C\) – через 8 минут, следовательно, остывал двигатель от \(90^\circ C\) до \(80^\circ C \ \) \(8-7=1\) минуту.

Найдите площадь заштрихованной фигуры, изображенной на клетчатой бумаге с размером клетки \(1\times 1\) .

Заметим, что закрашенная фигура состоит из четырех равных прямоугольных треугольников с катетами \(3\) и \(4\) . Следовательно, площадь равна \[S=4\cdot \left(\dfrac 12\cdot 3\cdot 4\right)=24\]

Фабрика выпускает сумки, причем в среднем на 141 качественную сумку приходится 9 сумок, имеющих скрытые дефекты. Найдите вероятность того, что случайно выбранная сумка не имеет скрытых дефектов.

Найдем вероятность того, что сумка имеет дефект. Для этого нужно количество дефектных сумок поделить на количество всех сумок. Всего 150 сумок, из них 9 с дефектом, следовательно, \[\dfrac9<150>=0,06\] Тогда вероятность того, что сумка без дефекта, равна \[1-0,06=0,94\]

Найдите корень уравнения \(\log_<\frac14>(2x+6)=-2\) .

ОДЗ уравнения: \(2x+6>0\) .
Уравнение можно переписать в виде: \[2x+6=\left(\frac14\right)^<-2>\quad\Leftrightarrow\quad 2x+6=16 \quad\Leftrightarrow\quad x=5\] Данный корень подходит по ОДЗ.

Периметр трапеции равен \(52\) , а радиус вписанной в нее окружности равен \(4\) . Найдите площадь этой трапеции.

Так как площадь любого многоугольника, в который вписана окружность, вычисляется по формуле \(S=p\cdot r\) , где \(p\) – полупериметр, \(r\) – радиус этой окружности, то \[S=\dfrac<52>2\cdot 4=104\]

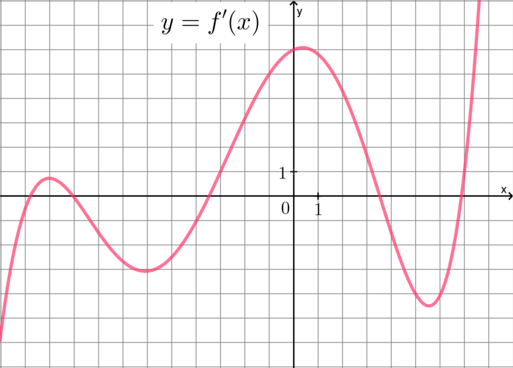
На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\) , определенной на интервале \((-12;7,6)\) . Найдите количество точек минимума функции \(f(x)\) , принадлежащих отрезку \([-10;4]\) .

Точки минимума – это точки, в которых функция меняет свой характер монотонности с убывания на возрастание. Следовательно, производная меняет свой знак с “ \(-\) ” на “ \(+\) ” (если смотреть слева направо). Таким образом, на графике нужно найти точки, в которых он пересекает ось абсцисс “снизу вверх” (если смотреть слева направо):

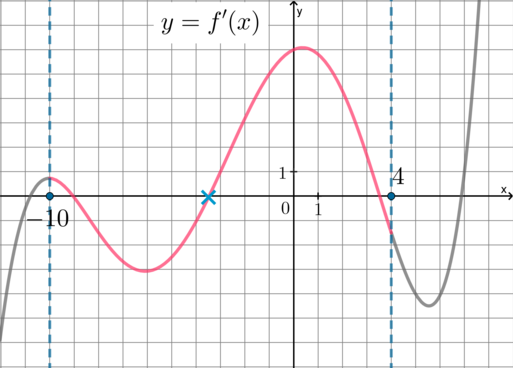
Следовательно, \(x=-4\) .

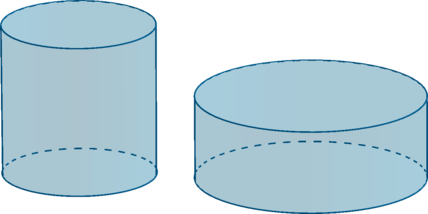
Первая цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.

Так как объем цилиндра равен произведению площади основания на высоту, то если принять за \(R\) – радиус основания первой кружки, \(h\) – высоту первой кружки, то ее объем равен \(V_1=\pi \cdot R^2\cdot h\) .
Из условия следует, что радиус основания второй кружки равен \(1,5R\) , высота второй кружки равна \(0,5h\) , следовательно, \(V_2=\pi \cdot (1,5R)^2\cdot 0,5h=1,125\cdot \pi\cdot R^2\cdot h\) . Тогда \[\dfrac=1,125\]

Так как \(\cos 2x=\cos^2x-\sin^2x\) , то числитель дроби можно преобразовать: \(7(\cos ^215^\circ-\sin^2 15^\circ)=7\cdot \cos 30^\circ\) . Так как \(\cos 30^\circ=\dfrac<\sqrt3>2\) , то \[\dfrac<7\cdot \frac<\sqrt3>2><\sqrt3>=\dfrac72=3,5\]

Для поддержания навеса планируется использовать цилиндрическую колонну. Давление \(P\) (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле \[P=\dfrac<4mg><\pi D^2>,\] где \(m=1350\) кг – общая масса навеса и колонны, \(D\) – диаметр колонны (в метрах). Считая ускорение свободного падения \(g=10\) м/с \(^2\) , а \(\pi=3\) , определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше \(200000\) Па. Ответ выразите в метрах.

Из условия задачи следует, что \(P\leqslant 200\,000\) . Подставим все значения из условия: \[\dfrac<4\cdot 1350\cdot 10><3\cdot D^2>\leqslant 200\,000 \quad\Rightarrow\quad D^2\geqslant \dfrac9<100>\quad\Rightarrow\quad D\geqslant \dfrac3<10>\] Следовательно, наименьший возможный диаметр равен \(D=0,3\) (м).

Первый сплав содержит \(10\%\) меди, второй – \(40\%\) меди. Масса второго сплава больше массы первого на \(3\) кг. Из этих двух сплавов получили третий сплав, содержащий \(30\%\) меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Пусть \(x\) – масса первого сплава, тогда \(x+3\) – масса второго. Так как два сплава смешали и получили третий сплав, то сумма меди в первом сплаве и меди во втором сплаве равна меди в третьем сплаве.
В первом сплаве меди \(0,1x\) кг, во втором – \(0,4 (x+3)\) кг, в третьем – \(0,3 (x+x+3)\) кг (так как третий сплав – сумма первых двух, то его масса равна сумме масс первого и второго сплавов).
Получаем уравнение \[0,1x+0,4 (x+3)=0,3 (2x+3)\quad\Leftrightarrow\quad x=3\] Тогда масса третьего сплава равна \(2\cdot 3+3=9\) кг.

Найдите точку максимума функции \(y=(x+16)\cdot e^<16-x>\) .

Найдем производную: \[y’=1\cdot e^<16-x>+(x+16)\cdot e^<16-x>\cdot (-1)=e^<16-x>\cdot (-x-15)\] Нуль производной: \(x=-15\) (так как \(e^<16-x>>0\) при любых \(x\) ).
Найдем знаки производной на двух получившихся промежутках:

Следовательно, по определению \(x=-15\) является точкой максимума (так как при \(x функция возрастает, при \(x>-15\) функция убывает).

а) Решите уравнение \(2\log^2_4(4\sin x)-5\log_4(4\sin x)+2=0\)

б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac<3\pi>2;0\right]\) .

а) Сделаем замену \(\log_4(4\sin x)=t\) , тогда уравнение примет вид: \[2t^2-5t+2=0\quad\Rightarrow\quad t_1=2; \quad t_2=\dfrac12\] Сделаем обратную замену:

1) \(\log_4(4\sin x)=2\quad\Rightarrow\quad 4\sin x=4^2\) – удовлетворяет ОДЗ логарифма \(4\sin x>0\) .
Полученное уравнение равносильно \(\sin x=4\) , что в свою очередь не имеет решений.

2) \(\log_4(4\sin x)=\frac12\quad\Rightarrow\quad 4\sin x=4^<\frac12>\) – также удовлетворяет ОДЗ.
Полученное уравнение равносильно \(\sin x=\frac12\) , решением которого будут \(x=\dfrac<\pi>6+2\pi n\) и \(x=\dfrac<5\pi>6+2\pi m\) , \(n,m\in\mathbb\) .

б) Отберем корни. 1) \(-\dfrac<3\pi>2\leqslant \dfrac<\pi>6+2\pi n\leqslant 0\quad\Leftrightarrow\quad -\dfrac56\leqslant n\leqslant -\dfrac1<12>\quad\Rightarrow\quad n\in\varnothing\quad\Rightarrow\quad x\in \varnothing\) 2) \(-\dfrac<3\pi>2\leqslant \dfrac<5\pi>6+2\pi m\leqslant 0\quad\Leftrightarrow\quad -\dfrac76\leqslant m\leqslant -\dfrac5<12>\quad\Rightarrow\quad m=-1\quad\Rightarrow\quad x=-\dfrac<7\pi>6\)

а) \(\dfrac<\pi>6+2\pi n, \ \dfrac<5\pi>6+2\pi m\) , \(n,m\in\mathbb\)

В основании правильной треугольной пирамиды \(ABCD\) лежит треугольник \(ABC\) со стороной, равной \(6\) . Боковое ребро пирамиды равно \(5\) . На ребре \(AD\) отмечена точка \(T\) так, что \(AT:TD=2:1\) . Через точку \(T\) параллельно прямым \(AC\) и \(BD\) проведена плоскость.

а) Докажите, что сечение пирамиды указанной плоскостью является прямоугольником.

б) Найдите площадь сечения.

а) Назовем плоскость из условия плоскостью \(\alpha\) . Так как она параллельна прямой \(AC\) , то \(\alpha\) пересечет плоскость \(ADC\) по прямой, параллельной прямой \(AC\) . Аналогично она пересечет плоскости \(ADB\) и \(CDB\) по прямым, параллельным \(BD\) .
Таким образом, проведем \(TK\parallel AC\) , \(KN\parallel BD\) , \(TM\parallel BD\) . \(MN\) также будет параллельно \(AC\) (так как \(AC\parallel \alpha\) ).

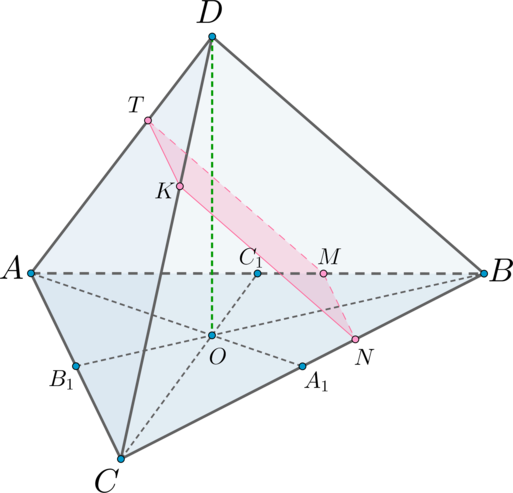
Получили сечение \(TMNK\) .
Докажем, что оно является прямоугольником.

1) Это параллелограмм, так как \(TK\parallel AC\parallel MN\) , \(TM\parallel BD\parallel KN\) .
Следовательно, осталось доказать, что, например, \(TM\perp MN\) .

2) Так как пирамида правильная, то в основании лежит правильный треугольник и высота пирамиды проходит через точку пересечения медиан (высот, биссектрис) основания. Следовательно, \(BB_1\perp AC\) , \(AC\parallel MN\) , отсюда \(MN\perp BB_1\) .

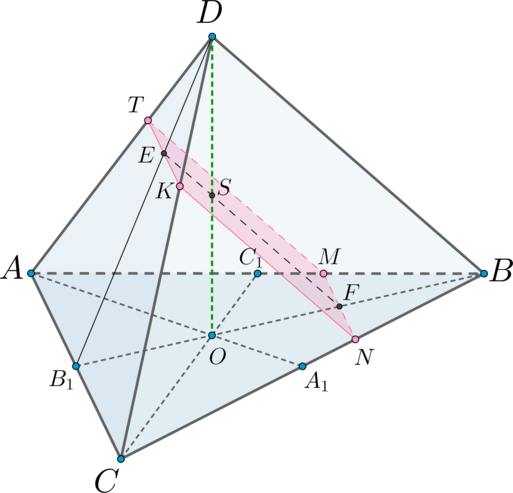
Пусть \(MN\cap BB_1=F\) , \(DB_1\cap TK=E\) . Тогда \(EF\) – линия пересечения плоскости \(\alpha\) и \((DBB_1)\) . Так как \(B_1\) – середина \(AC\) и \(TK\parallel AC\) , то \(E\) – середина \(TK\) . Аналогично \(F\) – середина \(MN\) . Следовательно, \(EF\parallel TM\) .
Значит, если мы докажем, что \(EF\perp MN\) , то и \(TM\perp MN\) .

3) Если \(S\) – точка пересечения \(DO\) и \(EF\) , то из теоремы о трех перпендикулярах, так как \(SO\perp (ABC)\) , \(OF\perp MN\) , следует, что \(SF\perp MN\) . Отсюда \(EF\perp MN\) . Чтд.

б) Нужно найти две смежные стороны \(TMNK\) , чтобы найти площадь.
Так как \(TM\parallel BD\) , то \(\triangle ATM\sim \triangle ADB\) , причем \(AT:AD=2:3\) . Следовательно, \(TM=\frac23DB=\frac<10>3\) .
Аналогично \(MN=\frac13AC=2\) .
Следовательно, \[S_=\dfrac<10>3\cdot 2=\dfrac<20>3\]

ОДЗ неравенства: \[\begin (x^2-8x+17)^2>0\\ (x^2-8x+17)^2\ne 1\\ 3x^2+5>0\\ x^2-8x+17>0\\ x^2-8x+17\ne 1\\ 2x^2+7x+5>0 \end \quad\Leftrightarrow\quad \begin x^2-8x+17\ne 0\\ x^2-8x+17\ne \pm 1\\ x^2>-\dfrac53\\[1ex] x^2-8x+17>0\\ x^2-8x+17\ne 1\\ 2x^2+7x+5>0 \end\quad\Leftrightarrow\quad \begin x^2>-\dfrac53\\[1ex] x^2-8x+17>0\\ x^2-8x+17\ne 1\\ 2x^2+7x+5>0 \end\] Так как \(x^2\geqslant 0\) при любом \(x\) , то решением первого неравенства будут \(x\in \mathbb\) .
Так как \(x^2-8x+17=(x-4)^2+1\) , то второе неравенство перепишется в виде \((x-4)^2>-1\) и его решением также будут \(x\in \mathbb\) .
\(x^2-8x+17\ne 1\) равносильно \((x-4)^2\ne 0\) , решением будут \(x\ne 4\) .
Неравенство \(2x^2+7x+5>0\) равносильно \(2(x+1)\left(x+\frac52\right)>0\) , следовательно, решением будут \(x\in \left(-\infty;-\frac52\right)\cup(-1;+\infty)\) .

Пересекая полученные решения, получаем, что ОДЗ: \[x\in \left(-\infty;-\frac52\right)\cup(-1;4)\cup(4;+\infty)\]

Решим неравенство на ОДЗ.
Его можно переписать в виде: \[\log_<(x^2-8x+17)>(3x^2+5)\leqslant \log_<(x^2-8x+17)>(2x^2+7x+5)\] Тогда по методу рационализации: \(\log_ab\geqslant \log_ac\quad\Rightarrow\quad (a-1)(b-c)\geqslant 0\) оно преобразуется в \[(x^2-8x+17-1)(3x^2+5-2x^2-7x-5)\geqslant 0 \quad\Leftrightarrow\quad (x-4)^2\cdot x(x-7)\geqslant 0\] Решим полученное неравенство методом интервалов:

Решением будут \(x\in [0;7]\) . Пересечем полученное решение с ОДЗ и получим окончательный ответ: \[x\in [0;4)\cup(4;7]\]

Окружность проходит через вершины \(B\) и \(C\) треугольника \(ABC\) и пересекает стороны \(AB\) и \(AC\) в точках \(C_1\) и \(B_1\) соответственно.

а) Докажите, что треугольник \(ABC\) подобен треугольнику \(AB_1C_1\) .

б) Вычислите длину стороны \(BC\) и радиус данной окружности, если \(\angle A=135^\circ\) , \(B_1C_1=10\) и площадь треугольника \(AB_1C_1\) в семь раз меньше площади четырехугольника \(BCB_1C_1\) .

а) Заметим, что эти треугольники имеют один общий угол – \(\angle A\) .

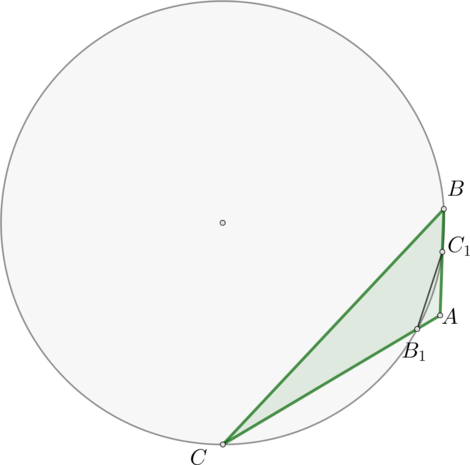
Докажем, что \(\angle ABC=\angle AB_1C_1\) . Тогда по признаку равенства по двум углам эти треугольники будут подобны.
\(\angle C_1BC+\angle C_1B_1C=180^\circ\) по свойству вписанного четырехугольника \(CBC_1B_1\) . Следовательно, \(\angle AB_1C_1=180^\circ-\angle C_1B_1C= 180^\circ-(180^\circ-\angle C_1BC)=\angle C_1BC\) . Чтд.

б) Пусть \(S_=S\) , тогда \(S_=7S\) . Следовательно, \(S_=8S\) . Тогда \(S_:S_=8:1\) . Так как эти треугольники подобны (доказано в пункте а), то это значит, что их коэффициент подобия равен \(k=\sqrt8=2\sqrt2\) .
Следовательно, \(BC=2\sqrt2B_1C_1=20\sqrt2\) .
Проведем \(OH\perp BC\) , \(OP\perp B_1C_1\) . Так как отрезок, проведенный из центра окружности перпендикулярно хорде, делит ее пополам, то \(HC=10\sqrt2\) , \(B_1P=5\) .
\(OC=OB_1=R\) – радиусы окружности.
Пусть большая дуга \(BC\) равна \(2\alpha\) , меньшая дуга \(B_1C_1\) равна \(2\beta\) . Тогда по свойству угла между двумя секущими \(135^\circ=\angle A=\alpha-\beta\) .

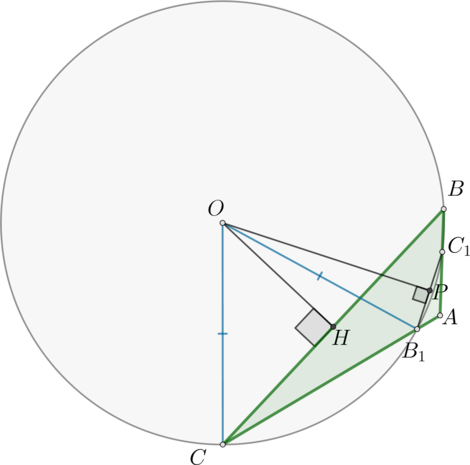
Тогда меньшая дуга \(BC\) равна \(\angle BOC\) и равна \(360^\circ-2\alpha\) , откуда \(\angle COH=180^\circ-\alpha\) . Тогда \(\angle OCH=\alpha-90^\circ\) .
Аналогично \(\angle B_1OC_1=2\beta\) , откуда \(\angle B_1OP=\beta\) .
Тогда : \[\begin \cos \angle OCH=\cos\angle (\alpha-90^\circ)=\dfrac<10\sqrt2>\\[2ex] \sin\angle B_1OP=\sin\angle \beta=\dfrac<5> \\[2ex] 135^\circ=\alpha-\beta\end \quad\Rightarrow\quad \begin 2\sqrt2\sin \beta=\sin\alpha \\ \alpha=\beta+135^\circ \end\] Тогда первое уравнение можно записать как: \(2\sqrt2\sin\beta=\sin (135^\circ+\beta)\) .
С помощью формулы \(\sin(x+y)=\sin x\cdot \cos y+\sin y\cdot \cos x\) можно получить уравнение \[2\sqrt2\sin \beta=\dfrac<\sqrt2>2(\cos \beta-\sin \beta) \quad\Rightarrow\quad \mathrm\,\beta=\dfrac<\sin \beta><\cos \beta>=\dfrac15\] Теперь рассмотрим \(\triangle B_1OP\) .
\(B_1P:OP=1:5\) , откуда \(OP=25\) . Следовательно, по теореме Пифагора, \[R=OB_1=5\sqrt<26>\]

Планируется взять кредит в банке на 25 месяцев. Условия его возврата таковы:
— 1 числа каждого месяца долг возрастает на \(10\%\) по сравнению с концом предыдущего месяца;
— со 2 по 14 число каждого месяца необходимо выплачивать часть долга;
— 15 числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 число предыдущего месяца.
Сколько рублей будет взято в банке, если известно, что общая сумма выплат после его погашения составит \(6957500\) рублей?

Из условия задачи следует, что система платежей дифференцированная. Общая сумма выплат по кредиту – это сумма всех платежей.
Пусть \(S\) – сумма, взятая в кредит.
Выпишем все платежи, учитывая, что они дифференцированные:

Следовательно, можно составить уравнение: \[\begin &\left(0,1\cdot S+\dfrac1<25>S\right)+\left(0,1\cdot \dfrac<24><25>S+\dfrac1<25>S\right)+\dots + \left(0,1\cdot \dfrac1<25>S+\dfrac1<25>S\right)=6957500\\[2ex] &0,1\cdot S\cdot \left(1+\dfrac<24><25>+\dots +\dfrac1<25>\right)+25\cdot \dfrac1<25>S=6957500 \end\] Так как в скобках находится арифметическая прогрессия, то найдем ее сумму по формуле \(S_<25>=\dfrac>2\cdot 25\) .
Так как \(a_1=1\) , \(a_<25>=\frac1<25>\) , тогда \[\begin &0,1\cdot S\cdot \left(\dfrac<1+\frac1<25>>2\cdot 25\right)+S=6957500\\[2ex] &0,1\cdot S\cdot 13+S=6957500\\[1ex] &S\cdot 2,3=6957500\\[1ex] &S=3025000 \end\]

Найдите все значения параметра \(a\) , при каждом из которых уравнение \[10a+\sqrt<-35+12x-x^2>=ax+1\]

имеет единственный корень.

Заметим, что \(-x^2+12x-35=-(x-6)^2+1\) . Поэтому перепишем уравнение в виде \[\sqrt<-(x-6)^2+1>=a(x-10)+1\] Рассмотрим две функции: \(y=\sqrt<-(x-6)^2+1>\) и \(g=a(x-10)+1\) .
При каждом фиксированном \(a\) графиком \(g\) является прямая, проходящая через точку \((10;1)\) .
Рассмотрим подробнее \(y\) . Заметим, что во-первых \(y\geqslant 0\) . Во-вторых, если возвести обе части в квадрат, получим \(y^2+(x-6)^2=1\) . Это уравнение окружности с центром в точке \((6;0)\) и радиусом \(1\) . Но так как \(y\geqslant 0\) , то графиком функции \(y\) является полуокружность (лежащая в верхней полуплоскости):

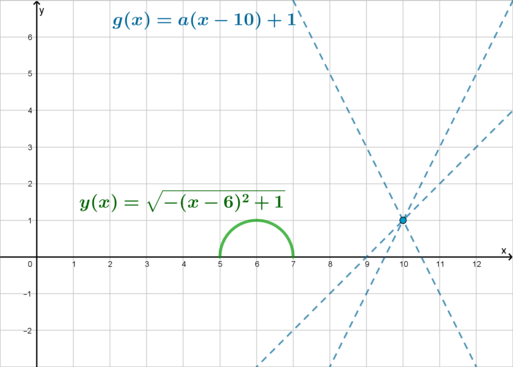
Нам нужно, чтобы графики имели ровно одну общую точку.
Рассмотрим случай (1), когда \(a=0\) . Тогда \(g=1\) и это прямая, параллельная оси абсцисс. Она будет касаться полуокружности в точке \((6;1)\) . Следовательно, это значение \(a\) нам подходит.
Когда прямая находится между положениями (1) и (2) (включая положение (2)), то она имеет 2 общие точки с полуокружностью.

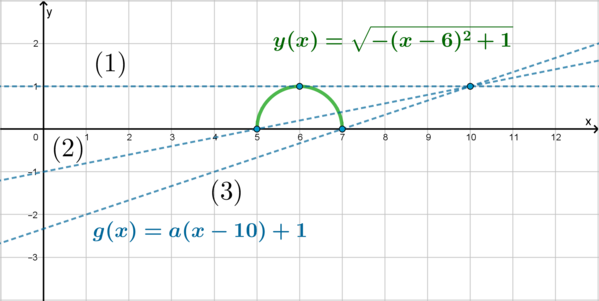
Находясь между положениями (2) и (3) (включая положение (3)), прямая имеет уже одну общую точку с полуокружностью. Следовательно, эти значения \(a\) нам подходят и их нужно найти.

Положение (2) – когда прямая проходит через точку \((5;0)\) : \(0=a(5-10)+1\) , откуда \(a=\frac15\) .

Положение (3) – когда прямая проходит через точку \((7;0)\) : \(0=a(7-10)+1\) , откуда \(a=\frac13\) .

Таким образом, \(a\in \<0\>\cup \left(\dfrac15; \dfrac13\right]\) .

Заметим, что во всех других положениях прямая не имеет с окружностью общих точек.

\(a\in \<0\>\cup \left(\frac15; \frac13\right]\)

Источник статьи: http://shkolkovo.net/variants/85