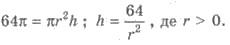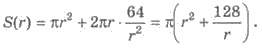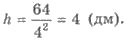1 забором длина которого 120 м надо огородить огород наибольшей площади найдите размеры огорода

АЛГЕБРА И НАЧАЛА АНАЛИЗА

§21. НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ. ПРИКЛАДНЫЕ ЗАДАЧИ НА НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ.

2. Прикладные задачи на нахождение наибольшего или (и) наименьшего значения некоторой величины.

При решении прикладных задач на нахождение наибольшего или (и) наименьшего значения некоторой величины можно использовать следующую схему:

1) Одну из величин обозначаем за х и по содержанию задачи накладываем ограничения на х.

2) Величину больше или (и) наименьшее значение которой требуется найти выражаем через х;

3) Находим наибольшее или (и) наименьшее значение полученной функции при наложенных ограничениях на х;

4) Выясняем какой практический смысл полученный результат.

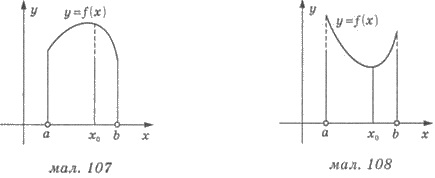
Заметим, что при решении некоторых практических задач необходимо найти больше или (и) наименьшее значение непрерывной функции на промежутке [а; b ], а на интервале (а; b ) . Как правило, в таких случаях на интервале (а; b ) функция имеет одну критическую точку. Если эта точка максимума, то именно в этой точке на интервале (а; b ) функция имеет наибольшее значение (рис. 107), а если это точка минимума, то меньше (рис. 108).

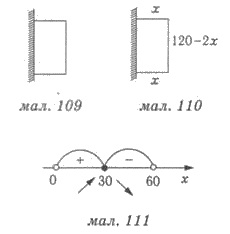
Пример 1. Забором, длина которого 120 м, надо огородить огород наибольшей площади (рис. 109). Найдите размеры огорода.

1) Обозначим через х м одну из двух параллельных сторон забора (рис. 110), тогда другая сторона будет равняться 120 — 2х (г), где 0 х 60.

2) Площадь огорода : S ( x ) = х(120 — 2х).

S ( x ) = 120х — 2 x 2 .

3) Найдем наибольшее значение функции :

S ( x ) = 120х — 2х 2 при условии х 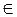(0;60).

S ‘( x )= 120 — 2 ∙ 2 x = 120 — 4 x ; S ‘( x ) = 0, когда х = 30 . Имеем х _{m ах} = 30 (рис. 111).

4) Поскольку S ( x ) = 120 — 2х 2 непрерывна на (0;60) и имеет точку максимума х _{m ах} = 30, то именно в этой точке S ( x ) достигает наибольшего значения. Следовательно, размер огорода 30 м и

120 — 2 ∙ 30 = 60 (м).

Пример 2. Необходимо изготовить открытый резервуар цилиндрической формы, объем которого равен 64 π дм 3 . При каких размерах резервуара (радиусу основания и высоте) на его изготовление тратится наименьшее количество металла?

1) Рассмотрим через r (дм) — радиус основания резервуара. Поскольку объем цилиндра V = π r 2 h , где h — высота, то имеем

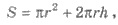
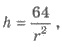
2) На изготовление резервуара расходуется такое количество металла π r 2 — площадь основания резервуара, 2 π rh — площадь боковой поверхности. Так то имеем

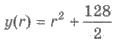
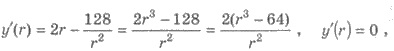
3) Найдем наименьшее значение функции при пусть r > 0.

когда r = 4. Имеем r_min = 4 (рис. 112).

4) Поскольку 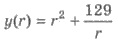непрерывная для r > 0 и имеет точку минимума r_min = 4, то именно в этой точке и в( r ), а потому и S ( r ) достигает наименьшего значения. Следовательно, радиус основания цилиндра равен 4 дм, высота

1 забором длина которого 120 м надо огородить огород наибольшей площади найдите размеры огорода

Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 30 м и 75 м. Найдите длину забора, которым нужно огородить участок, предусмотрев проезд шириной 3 м. Ответ дайте в метрах.

Забор представляет собой прямоугольник с отсутствующим кусочком на одной из сторон. Периметр данного прямоугольника без учёта проёма: м. Учитывая длину проёма, получим, что длина забора: м.

Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 35 м и 60 м. Найдите длину забора, которым нужно огородить участок, предусмотрев проезд шириной 4 м. Ответ дайте в метрах.

Забор представляет собой прямоугольник с отсутствующим кусочком на одной из сторон. Периметр данного прямоугольника без учёта проёма: м. Учитывая длину проёма, получим, что длина забора: м.

Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 50 м. Найдите длину забора, которым нужно огородить участок, предусмотрев проезд шириной 3 м. Ответ дайте в метрах.

Забор представляет собой прямоугольник с отсутствующим кусочком на одной из сторон. Периметр данного прямоугольника без учёта проёма: м. Учитывая длину проёма, получим, что длина забора: м.

Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 65 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.

Забор представляет собой прямоугольник с отсутствующим кусочком на одной из сторон. Периметр данного прямоугольника без учёта проёма: 2(65+ 25) = 180 м. Учитывая длину проёма, получим, что длина забора: 180 − 4 = 176 м.

Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 35 м и 70 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.

Забор представляет собой прямоугольник с отсутствующим кусочком на одной из сторон. Периметр данного прямоугольника без учёта проёма: 2(70 + 35) = 210 м. Учитывая длину проёма, получим, что длина забора: 210 − 4 = 206 м.

Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 40 м и 55 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 3 м.

Забор представляет собой прямоугольник с отсутствующим кусочком на одной из сторон. Периметр данного прямоугольника без учёта проёма: 2(40+ 55) = 190 м. Учитывая длину проёма, получим, что длина забора: 190 − 3 = 187 м.

Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 30 м и 40 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 3 м.

Забор представляет собой прямоугольник с отсутствующим кусочком на одной из сторон. Периметр данного прямоугольника без учёта проёма: 2(40+ 30) = 140 м. Учитывая длину проёма, получим, что длина забора: 140 − 3 = 137 м.

Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 1000 м и 600 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.

Длина забора — сумма длин двух коротких сторон и одной длинной стороны: 600 + 600 + 1000 = 2200.

Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 800 м и 300 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.

Длина забора — сумма длин двух коротких сторон и одной длинной стороны: 300 + 300 + 800 = 1400.

Участок земли для строительства дачи имеет форму прямоугольника, стороны которого равны 40 м и 30 м. Одна из больших сторон участка идёт вдоль реки, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.

Длина забора — сумма длин двух коротких сторон и одной длинной стороны: 30 + 30 + 40 = 100.

Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 30 м и 45 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 3 м.

Забор представляет собой прямоугольник с отсутствующим кусочком на одной из сторон. Периметр данного прямоугольника без учёта проёма: 2(45+ 30) = 150 м. Учитывая длину проёма, получим, что длина забора: 150 − 3 = 147 м.

Прямоугольный участок земли имеет стороны 28 и 40 м. Короткой стороной участок примыкает к стене дома. Найдите длину забора, которым нужно огородить оставшуюся часть границы участка (в метрах).

Длина забора — сумма длин двух длинных сторон и одной короткой стороны: 40 + 40 + 28 = 108 метров.

Прямоугольный участок земли имеет стороны 35 и 45 м. Короткой стороной участок примыкает к стене дома. Найдите длину забора, которым нужно огородить оставшуюся часть границы участка (в метрах).

Длина забора — сумма длин двух длинных сторон и одной короткой стороны: 45 + 45 + 35 = 125 метров.

Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 1000 м и 500 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно оградить забором. Найдите длину этого забора. Ответ дайте в метрах.

Из свойств прямоугольника известно, что противоположные стороны равны. Наибольшая сторона — м, она идет вдоль моря. Сумма длин оставшихся сторон м.

Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 1000 м и 500 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.

Из свойств прямоугольника известно, что противоположные стороны равны. Наибольшая сторона — м, она идет вдоль моря. Сумма длин оставшихся сторон м.

Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 1000 м и 600 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.

Из свойств прямоугольника известно, что противоположные стороны равны. Наибольшая сторона — м, она идет вдоль моря. Сумма длин оставшихся сторон м.

Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 40 м и 30 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.

Из свойств прямоугольника известно, что противоположные стороны равны. Наибольшая сторона — м, она идет вдоль моря. Сумма длин оставшихся сторон м.

Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 50 м и 30 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.

Из свойств прямоугольника известно, что противоположные стороны равны. Наибольшая сторона — м, она идет вдоль моря. Сумма длин оставшихся сторон м.

Дачный участок имеет форму прямоугольника со сторонами 25 метров и 15 метров. Хозяин планирует обнести его изгородью и отгородить такой же изгородью квадратный участок со стороной 8 м (см. рис.). Найдите суммарную длину изгороди в метрах.

Длина забора равна сумме периметров двух заборов. Найдем периметр участка 25 + 25 + 15 + 15 = 80 м.

1 забором длина которого 120 м надо огородить огород наибольшей площади найдите размеры огорода

Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин отгородил на участке квадратный вольер со стороной 15 метров (см. рисунок). Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.

Площадь квадрата равна квадрату его стороны, поэтому площадь вольера равна 15 · 15 = 225 кв.м. Площадь прямоугольника равна произведению его длины на ширину, поэтому площадь участка равна 30 · 25 = 750 кв.м. Тем самым, площадь оставшейся части участка равна 750 − 225 = 525 кв.м.

Дачный участок имеет форму прямоугольника со сторонами 30 метров и 20 метров. Хозяин отгородил на участке квадратный вольер со стороной 12 метров (см. рисунок). Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.

Площадь квадрата равна квадрату его стороны, поэтому площадь вольера равна 12 · 12 = 144 кв.м. Площадь прямоугольника равна произведению его длины на ширину, поэтому площадь участка равна 30 · 20 = 600 кв.м. Тем самым, площадь оставшейся части участка равна 600 − 144 = 456 кв.м.

Аналоги к заданию № 511901: 512496 512516 512536 512556 Все

Прямолинейный участок трубы длиной 3 м, имеющей в сечении окружность, необходимо покрасить снаружи (торцы трубы открыты, их красить не нужно). Найдите площадь поверхности, которую необходимо покрасить, если внешний обхват трубы равен 32 см. Ответ дайте в квадратных сантиметрах.

Переведём длину участка трубы в сантиметры: 3 м = 300 см. Площадь поверхности цилиндра равняется см 2 .